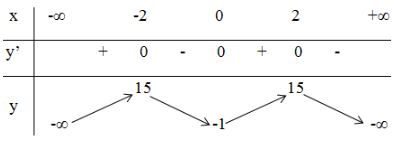
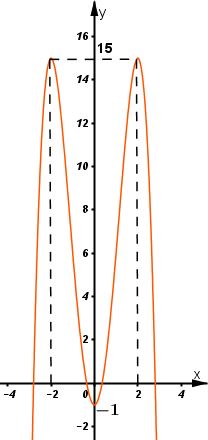
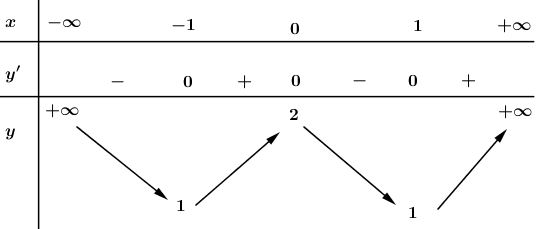
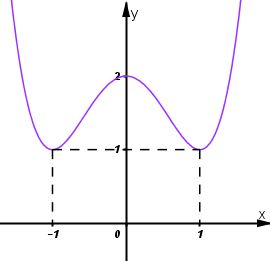
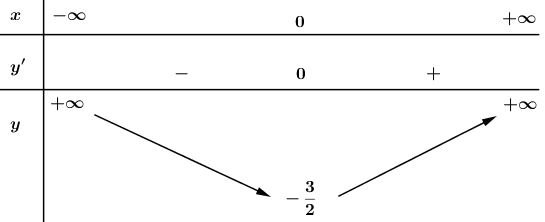
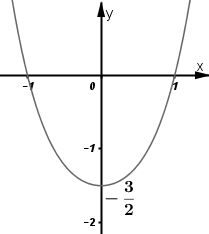
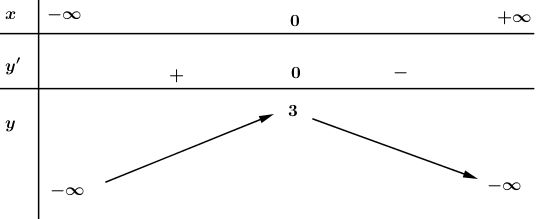
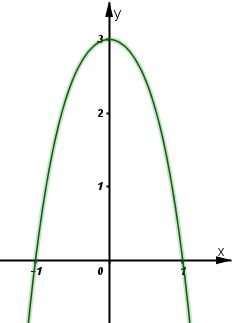
Giải bài 2 trang 43 SGK Giải tích 12

LG a

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:

$y=- {x^4} + 8{x^{2}}-1$;

Phương pháp giải:

Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:

Bước 1: Tìm TXĐ của hàm số.

Bước 2: Khảo sát sự biến thiên:

*) Xét chiều biến thiên của hàm số:

+) Tính đạo hàm.

+) Tìm các điểm ${{x}_{i}}$ mà tại đó đạo hàm có $y'=0$ hoặc đạo hàm không xác định.

+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

*) Tìm cực trị: $y\left( {{x}_{i}} \right).$

*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số nếu có: $\mathop {\lim }\limits_{x \to  \pm \infty } y;\mathop {\lim }\limits_{x \to {x_0}} y...$ 

*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

Bước 3: Đồ thị:

+) Giao điểm của đồ thị với trục tung: $x=0\Rightarrow y=....\Rightarrow A\left( 0;\ ..... \right).$

+) Giao điểm của đồ thị với trục hoành: $y=0\Rightarrow x=.....\Rightarrow B\left( ...;0 \right).$

+) Các điểm cực đại, cực tiểu nếu có.

Lời giải chi tiết:

Tập xác định: $D=\mathbb R$;

Sự biến thiên:

Ta có: $y' =-4x^3+ 16x = -4x(x^2- 4)$

$\Rightarrow y' = 0 \Leftrightarrow - 4x\left( {{x^2} - 4} \right) = 0$ $\Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 2\end{array} \right.$

- Hàm số đồng biến trên khoảng $(-\infty;-2)$ và $(0;2)$; nghịch biến trên khoảng $(-2;0)$ và $2;+\infty)$.

- Cực trị:

    Hàm số đạt cực đạt tại hai điểm $x=-2$ và $x=2$; $y_{CĐ}=y(\pm 2)=15$.

    Hàm số đạt cực tiểu tại $x=0$; $y_{CT}=-1$

- Giới hạn: $\mathop {\lim y}\limits_{x \to  \pm \infty }  =  - \infty$

Bảng biến thiên:

Đồ thị giao $Oy$ tại điểm $(0;-1)$

Hàm số đã cho là hàm số chẵn nhận trục $Oy$ làm trục đối xứng.

Đồ thị 

LG b

$y= {x^4} - 2{x^2} + 2$;

Lời giải chi tiết:

Tập xác định: $D=\mathbb R$;

Sự biến thiên:

Ta có: $y' =4x^3- 4x = 4x(x^2- 1)$;

$\Rightarrow y' = 0 \Leftrightarrow 4x\left( {{x^2} - 1} \right) = 0$ $\Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} - 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \pm 1 \end{array} \right..$

- Hàm số đồng biến trên khoảng $(-1;0)$ và $(1;+\infty)$; nghịch biến trên khoảng $(-\infty;-1)$  và $(0;1)$.

- Cực trị: 

    Hàm số đạt cực đại tại $x=0$; $y_{CĐ}=2$.

    Hàm số đạt cực tiểu tại hai điểm $x=-1$ và $x=1$; $y_{CT}=y(\pm 1)=1$.

-Giới hạn:

$\mathop {\lim y}\limits_{x \to  \pm \infty }  =  + \infty$

Bảng biến thiên:

Hàm số đã cho là hàm số chẵn nhận trục $Oy$ làm trục đối xứng.

Đồ thị giao $Oy$ tại điểm $(0;2)$

Đồ thị 

LG c

$y = {1 \over 2}{x^4} + {x^2} - {3 \over 2}$;

Lời giải chi tiết:

Tập xác định: $D=\mathbb R$;

Sự biến thiên:

Ta có: $y' =2x^3+ 2x = 2x(x^2+1)$;

$\Rightarrow y' = 0 \Leftrightarrow 2x\left( {{x^2} + 1} \right) = 0$ $\Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} + 1 = 0 \end{array} \right. \Leftrightarrow x = 0.$

- Hàm số nghịch biến trên khoảng $(-\infty;0)$; đồng biến trên khoảng $(0;+\infty)$.

-Cực trị:

    Hàm số đạt cực tiểu tại $x=0$; $y_{CT}={-3\over 2}$

-Giới hạn:

$\mathop {\lim y}\limits_{x \to  \pm \infty }  =  + \infty$

Bảng biến thiên :

Hàm số đã cho là hàm số chẵn, nhận trục $Oy$ làm trục đối xứng.

Đồ thị giao $Ox$ tại hai điểm $(-1;0)$ và $(1;0)$; giao $Oy$ tại $(0;{-3\over 2})$.

Đồ thị như hình bên.

LG d

 $y =  - 2{x^2} - {x^4} + 3$.

Lời giải chi tiết:

Tập xác định: $D=\mathbb R$;

Sự biến thiên:

Ta có: $y' = -4x - 4x^3= -4x(1 + x^2)$;

$\Rightarrow y' = 0 \Leftrightarrow - 4x\left( {1 + {x^2}} \right) = 0$ $\Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} + 1 = 0 \end{array} \right. \Leftrightarrow x = 0.$

- Hàm số đồng biến trên khoảng: $(-\infty;0)$; nghịch biến trên khoảng: $(0;+\infty)$.

- Cực trị: Hàm số đạt cực đạt tại $x=0$; $y_{CĐ}=3$.

- Giới hạn: 

$\mathop {\lim y}\limits_{x \to  \pm \infty }  =  -\infty$

Bảng biến thiên:

Hàm số đã cho là hàm chẵn, nhận trục $Oy$ làm trục đối xứng.

Đồ thị giao $Ox$ tại hai điểm $(1;0)$ và $(-1;0)$; giao $Oy$ tại điểm $(0;3)$.

 Đồ thị như hình bên.

HocTot.Nam.Name.Vn