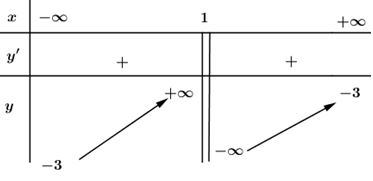
Giải bài 2 trang 10 SGK Giải tích 12

LG a

a) $y=\dfrac{3x+1}{1-x}$ ;

Phương pháp giải:

+) Tìm tập xác định của hàm số.

+) Tính đạo hàm của hàm số. Tìm các điểm x_i (I =1,2,3,…,n) mà tại đó đạo hàm bằng 0 hoặc không xác định

+) Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên

+) Dựa vào bảng biến thiên để kết luận khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó. (nếu y’ > 0 thì hàm số đồng biến, nếu y’ < 0 thì hàm số nghịch biến)

Ở bài toán này cần chú ý các tập xác định của hàm số.

Lời giải chi tiết:

$y=\dfrac{3x+1}{1-x}=\dfrac{3x+1}{-x+1}$        

Tập xác định: $D=R\backslash \left\{ 1 \right\}.$

Có: $y'=\dfrac{3.1-(-1).1}{{{\left( -x+1 \right)}^{2}}}$$=\dfrac{4}{{{\left( -x+1 \right)}^{2}}}>0\ \forall \ x\in D.$

Bảng biến thiên:

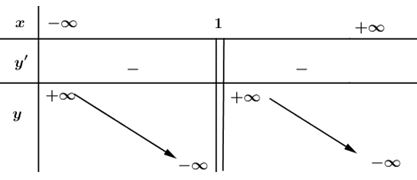
Vậy hàm số đồng biến trên các khoảng xác định của nó là: $\left( -\infty ;\ 1 \right)$ và $\left( 1;+\infty  \right).$

Chú ý: Cách tính giới hạn để điền vào BBT: $\mathop {\lim }\limits_{x \to  \pm \infty } \dfrac{{3x + 1}}{{1 - x}} =  - 3,$ $\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{3x + 1}}{{1 - x}} =  - \infty ,$ $\mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{3x + 1}}{{1 - x}} =  + \infty$            

Quảng cáo

LG b

b) $y=\dfrac{x^{2}-2x}{1-x}$ ;

Lời giải chi tiết:

$y=\dfrac{{{x}^{2}}-2x}{1-x}.$

Tập xác định: $D=R\backslash \left\{ 1 \right\}.$

Có: $y'=\dfrac{\left( 2x-2 \right)\left( 1-x \right)+{{x}^{2}}-2x}{{{\left( 1-x \right)}^{2}}}$ $=\dfrac{-{{x}^{2}}+2x-2}{{{\left( 1-x \right)}^{2}}}$ $=\dfrac{-\left( {{x}^{2}}-2x+2 \right)}{{{\left( 1-x \right)}^{2}}}$ $=\dfrac{-\left( {{x}^{2}}-2x+1 \right)-1}{{{\left( 1-x \right)}^{2}}}$ $=\dfrac{-{{\left( x-1 \right)}^{2}}-1}{{{\left( 1-x \right)}^{2}}}$ $=-1-\dfrac{1}{{{\left( 1-x \right)}^{2}}}<0\ \forall x\in D.$

Bảng biến thiên:

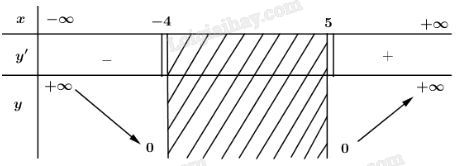
Vậy hàm số nghịch biến trên các khoảng xác định của nó là: $\left( -\infty ;\ 1 \right)$ và $\left( 1;+\infty  \right).$

Chú ý: Cách tính giới hạn để điền vào bảng biến thiên:

$\begin{align}& \underset{x\to +\infty }{\mathop{\lim }}\,\dfrac{{{x}^{2}}-2x}{1-x}=-\infty \cr& \underset{x\to -\infty }{\mathop{\lim }}\,\dfrac{{{x}^{2}}-2x}{1-x}=+\infty \  \\ & \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\dfrac{3x+1}{1-x}=+\infty \cr&\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\dfrac{3x+1}{1-x}=-\infty  \\ \end{align}$

LG c

c) $y=\sqrt{x^{2}-x-20}$ ;   

Lời giải chi tiết:

$y=\sqrt{{{x}^{2}}-x-20}$                     

Có ${{x}^{2}}-x-20\ge 0$ $\Leftrightarrow \left( x+4 \right)\left( x-5 \right)\ge 0$ $\Leftrightarrow \left[ \begin{align} & x\le -4 \\ & x\ge 5 \\ \end{align} \right..$

Tập xác định: $D=\left( -\infty ;-4 \right]\cup \left[ 5;+\infty  \right).$

Có $y'=\dfrac{2x-1}{2\sqrt{{{x}^{2}}-x-20}}$ $\Rightarrow y'=0\Leftrightarrow 2x-1=0$$\Leftrightarrow x=\dfrac{1}{2}\notin D$

Bảng biến thiên:

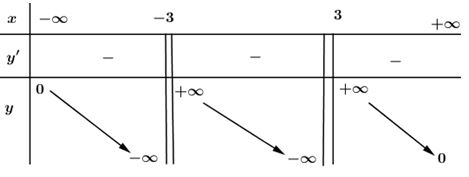
Vậy hàm số nghịch biến trên khoảng $\left( -\infty ;-4 \right)$ và đồng biến trên khoảng $\left( 5;+\infty  \right).$

Chú ý: Cách tính giới hạn để điền vào BBT:

$\begin{align}  & \underset{x\to -\infty }{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=+\infty\cr&\underset{x\to +\infty }{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=+\infty  \\  & \underset{x\to {{4}^{-}}}{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=0\cr& \underset{x\to {{5}^{+}}}{\mathop{\lim }}\,\sqrt{{{x}^{2}}-x-20}=0.\  \\ \end{align}$

LG d

d) $y=\dfrac{2x}{x^{2}-9}$.

Lời giải chi tiết:

$y=\dfrac{2x}{{{x}^{2}}-9}.$

Có ${{x}^{2}}-9\ne 0\Leftrightarrow x\ne \pm 3.$

Tập xác định:  $D=R\backslash \left\{ \pm 3 \right\}.$

Có: $y'=\dfrac{2\left( {{x}^{2}}-9 \right)-2x.2x}{{{\left( {{x}^{2}}-9 \right)}^{2}}}$ $=\dfrac{-2{{x}^{2}}-18}{{{\left( {{x}^{2}}-9 \right)}^{2}}}$ $=\dfrac{-2\left( {{x}^{2}}+9 \right)}{{{\left( {{x}^{2}}-9 \right)}^{2}}}<0\ \forall \ x\in D.$

Bảng biến thiên:

Vậy hàm số nghịch biến trên các khoảng xác định của nó là: $\left( -\infty ;\ -3 \right);\ \left( -3;\ 3 \right)$ và $\left( 3;\ +\infty  \right).$

Chú ý: Cách tính giới hạn để điền vào BBT:

$\begin{align}& \underset{x\to -\infty }{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=0\cr&\underset{x\to +\infty }{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=0 \\ & \underset{x\to -{{3}^{+}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=+\infty \cr&\underset{x\to -{{3}^{-}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=-\infty  \\ & \underset{x\to {{3}^{+}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=+\infty \cr& \underset{x\to {{3}^{-}}}{\mathop{\lim }}\,\dfrac{2x}{{{x}^{2}}-9}=-\infty . \\ \end{align}$

HocTot.Nam.Name.Vn