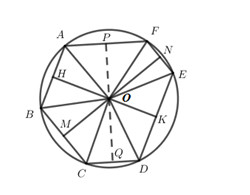
Bài 16 trang 80 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Cho lục giác lồi ABCDEF có các đỉnh nằm trên một đường tròn và có hai cặp cạnh đối song song AB // DE, BC // EF. Chứng minh rằng cặp cạnh đối còn lại cũng song song với nhau.

Lời giải chi tiết

 

Gọi H, K lần lượt là trung điểm của AB và DE ta có:

$OH \bot AB;\,\,OK \bot DE$(quan hệ vuông góc giữa đường kính và dây cung)

Lại có $AB//DE\,\,\left( {gt} \right) \Rightarrow OH \bot DE$

Từ O ta có thể kẻ hai đường thẳng OH và OK cùng vuông góc với DE $\Rightarrow O;H;K$thẳng hàng.

Gọi M, N lần lượt là trung điểm của BC và EF. Chứng minh tương tự ta có O, M, N thẳng hàng.

$\Rightarrow \widehat {HOM} = \widehat {NOK}$ (đối đỉnh).

Xét tam giác OAB có $\left\{ \begin{array}{l}OA = OB = R\\OH \bot AB\end{array} \right. \Rightarrow \widehat {AOH} = \widehat {BOH} = \dfrac{1}{2}\widehat {AOB}$

Xét tam giác OBC có $\left\{ \begin{array}{l}OB = OC = R\\OM \bot BC\end{array} \right. \Rightarrow \widehat {BOM} = \widehat {COM} = \dfrac{1}{2}\widehat {BOC}$

$\Rightarrow \widehat {AOB} + \widehat {BOC} = 2\widehat {BOH} + 2\widehat {BOM} = 2\widehat {HOM}$ $\Leftrightarrow \widehat {AOC} = 2\widehat {HOM}$

Chứng minh tương tự ta có $\widehat {FOD} = 2\widehat {NOK}$

Mà $\widehat {HOM} = \widehat {NOK}\,\,\left( {cmt} \right) \Rightarrow \widehat {AOC} = \widehat {FOD}\,\,\left( 1 \right)$.

Gọi P, Q lần lượt là trung điểm của AE và CD.

Tam giác OAF cân tại O $\left( {OA = OF = R} \right) \Rightarrow OP \bot AF \Rightarrow$ Đường cao OP đồng thời là phân giác $\Rightarrow \widehat {AOP} = \widehat {FOP}$  (2)

Chứng minh tương tự ta có $\widehat {COQ} = \widehat {DOQ}\,\,\,\left( 3 \right)$.

Từ (1), (2) và (3) $\Rightarrow \widehat {AOC} + \widehat {AOP} + \widehat {COQ} = \widehat {FOD} + \widehat {FOP} + \widehat {DOQ}$

$\Rightarrow \widehat {POQ} = {180^0}$

$\Rightarrow O;P;Q$ thẳng hàng.

$\Rightarrow OP \bot CD$.

Vậy $AF//CD$ (cùng vuông góc với OP).

 HocTot.Nam.Name.Vn