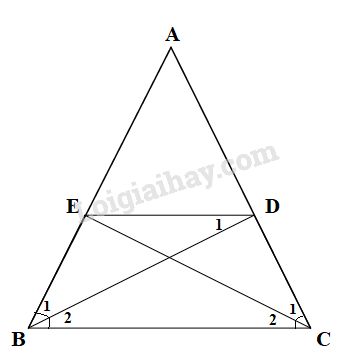
Bài 16 trang 75 SGK Toán 8 tập 1

Đề bài

Cho tam giác $ABC$ cân tại $A$, các đường phân giác $BD, CE$ ($D ∈ AC, E ∈ AB$). Chứng minh rằng $BEDC$ là hình thang cân có đáy nhỏ bằng cạnh bên.

Lời giải chi tiết

 

$\Delta ABC$ cân tại $A$ (giả thiết)

$\Rightarrow \left\{ \begin{array}{l} AB = AC\\ \widehat {ABC} = \widehat {ACB} \end{array} \right.$  (tính chất tam giác cân)

Vì $BD, CE$ lần lượt là phân giác của $\widehat {ABC}$ và $\widehat {ACB}$ (giả thiết) 

$\Rightarrow \left\{ \begin{array}{l} \widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\\ \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat {ACB}}}{2} \end{array} \right.$ (tính chất tia phân giác)

Mà $\widehat {ABC} = \widehat {ACB}$ (chứng minh trên)

$\Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}$

 Xét $∆ABD$ và  $∆ACE$ có:

+) $AB = AC$ (chứng minh trên)

+) $\widehat{A}$ chung

+) $\widehat {{B_1}} = \widehat {{C_1}}$ (chứng minh trên)

$\Rightarrow \Delta ABD = \Delta ACE{\rm{ }}\left( {g.c.g} \right)$

$\Rightarrow A{\rm{D}} = A{\rm{E}}$ ($2$ cạnh tương ứng).

Ta có $AD =  AE$ (chứng minh trên) nên  $∆ADE$ cân tại $A$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat {A{\rm{ED}}} = \widehat {AD{\rm{E}}}$ (tính chất tam giác cân)

Xét $∆ADE$ có:  $\widehat {A{\rm{ED}}} + \widehat {AD{\rm{E}}} + \widehat A = {180^0}$ (định lý tổng ba góc trong tam giác)

$\begin{array}{l} \Rightarrow 2\widehat {A{\rm{ED}}} + \widehat A = {180^0}\\ \Rightarrow \widehat {A{\rm{ED}}} = \dfrac{{{{180}^0} - \widehat A}}{2}\left( 1 \right) \end{array}$

Xét $∆ABC$ có: $\widehat A +\widehat {ABC} + \widehat {ACB} = {180^0}$ (định lý tổng ba góc trong tam giác)

Mà $\widehat {ABC} = \widehat {ACB}$ (chứng minh trên)

$\begin{array}{l} \Rightarrow \widehat {2ABC} + \widehat A = {180^0}\\ \Rightarrow \widehat {ABC}= \dfrac{{{{180}^0} - \widehat A}}{2}\left( 2 \right) \end{array}$

Từ (1) và (2) $\Rightarrow \widehat{A{\rm{ED}}}$ = $\widehat{ABC}$, mà hai góc này là hai góc đồng vị nên suy ra $DE // BC$ (dấu hiệu nhận biết hai đường thẳng song song)

Do đó $BEDC$ là hình thang (dấu hiệu nhận biết hình thang).

Lại có $\widehat{ABC}$ = $\widehat{ACB}$  (chứng minh trên)

Nên $BEDC$ là hình thang cân (dấu hiệu nhận biết hình thang cân)

Ta có:

$DE//BC \Rightarrow \widehat {{D_1}} = \widehat {{B_2}}$ (so le trong)

Lại có $\widehat{B_{2}}$ = $\widehat{B_{1}}$ (chứng minh trên) nên $\widehat{B_{1}}$ = $\widehat{{D_{1}}}$

$\Rightarrow \Delta EB{\rm{D}}$ cân tại $E$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow EB = E{\rm{D}}$ (tính chất tam giác cân).

Vậy $BEDC$ là hình thang cân có đáy nhỏ bằng cạnh bên.

HocTot.Nam.Name.Vn