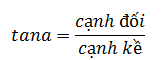Bài 1.16 trang 19 SGK Toán 11 tập 1 - Cùng khám phá

Đề bài

Một vận động viên bắn súng nằm trên mặt đất để ngắm bắn các mục tiêu khác nhau trên một bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất 20 m tại một góc ngắm (góc hợp bởi phương bắn và phương ngang). Nếu tăng góc ngắm đó lên hai lần thì vận động viên bắn trúng một mục tiêu cách mặt đất 45 m. Tính khoảng cách từ vận động viên đến bức tường.

Quảng cáo

Lời giải chi tiết

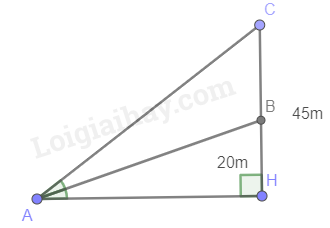
Gọi A là vị trí vận động viên nằm, B là mục tiêu cách mặt đất 20m, C là mục tiêu cách mặt đất 45m và H như trên hình

\(\begin{array}{l}\tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{{20}}{{AH}}\\\tan \widehat {CAH} = \frac{{CH}}{{AH}} = \frac{{45}}{{AH}}\\\widehat {CAH} = 2\widehat {BAH}\\ \Rightarrow \tan \left( {2.\widehat {BAH}} \right) = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{2\tan \widehat {BAH}}}{{1 - {{\tan }^2}\widehat {BAH}}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \left( {2.\frac{{20}}{{AH}}} \right):\left[ {1 - {{\left( {\frac{{20}}{{AH}}} \right)}^2}} \right] = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}:\left( {1 - \frac{{400}}{{A{H^2}}}} \right) = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}:\frac{{A{H^2} - 400}}{{A{H^2}}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}.\frac{{A{H^2}}}{{A{H^2} - 400}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40AH}}{{A{H^2} - 400}} = \frac{{45}}{{AH}}\\ \Leftrightarrow 40A{H^2} = 45A{H^2} - 18000\\ \Leftrightarrow A{H^2} = 3600\\ \Rightarrow AH = 60\end{array}\)