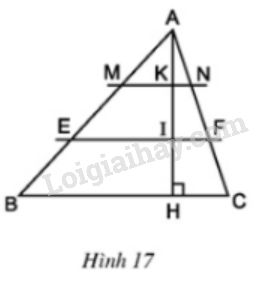
Bài 11 trang 63 SGK Toán 8 tập 2

LG a.

Tính độ dài đoạn thẳng \(MN\) và \(EF\).

Phương pháp giải:

Áp dụng: Hệ quả của định lý TaLet, áp dụng kết quả của bài 10.

Lời giải chi tiết:

\(∆ABC\) có \(MN // BC\) (gt)

\( \Rightarrow \dfrac{MN}{CB} = \dfrac{AK}{AH}\) (kết quả bài tập 10) (định lý TaLet)

Mà \(AK = KI = IH\).

Nên \(\dfrac{AK}{AH} = \dfrac{1}{3}\) 

\( \Rightarrow \dfrac{MN}{CB} = \dfrac{1}{3}\) 

\( \Rightarrow  MN = \dfrac{1}{3}BC = \dfrac{1}{3}.15 = 5\, cm\).

\(∆ABC\) có \(EF // BC\) (gt)

\( \Rightarrow \dfrac{EF}{BC} = \dfrac{AI}{AH} = \dfrac{2}{3}\) (định lý TaLet)

\(\Rightarrow  EF =\dfrac{2}{3}.BC= \dfrac{2}{3}.15 =10 \,cm\).

LG b.

Tính diện tích tứ giác \(MNFE\), biết diện tích của \(∆ABC\) là \(270\) cm²

Phương pháp giải:

Áp dụng: Hệ quả của định lý TaLet, áp dụng kết quả câu a.

Lời giải chi tiết:

Theo câu a) ta có: \(AK=\dfrac{1}{3}AH;MN=\dfrac{1}{3}BC;\) \(AI=\dfrac{2}{3}AH;EF=\dfrac{2}{3}BC\)

Nên:

\(\eqalign{
& {S_{AMN}} = {1 \over 2}.AK.MN \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 9}.{S_{ABC}} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 9}.270 = 30\,c{m^2} \cr} \)

\(\eqalign{
& {S_{AEF}} = {1 \over 2}.AI.EF \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}.{2 \over 3}AH.{2 \over 3}BC \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {4 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {4 \over 9}.{S_{ABC}} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {4 \over 9}.270 = 120\,c{m^2} \cr} \)

Do đó \({S_{MNFE}} = {S_{AEF}} - {S_{AMN}} = 120 - 30 \)\(\,= 90c{m^2}\)

HocTot.Nam.Name.Vn