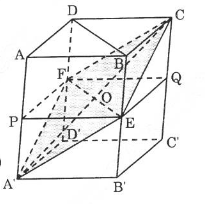
Bài 11 trang 27 SGK Hình học 12

Đề bài

Cho hình hộp $ABCD.A'B'C'D'$. Gọi $E$ và $F$ theo thứ tự là trung điểm của các cạnh $BB'$ và $DD'$. Mặt phẳng $(CEF)$ chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.

Lời giải chi tiết

Ta xác định thiết diện của hình hộp $\displaystyle ABCD.A'B'C'D'$ khi cắt bởi $\displaystyle (CEF)$. Mặt phẳng $\displaystyle (CEF)$ chứa đường thẳng $\displaystyle EF$ mà $\displaystyle E$ là trung điểm của $\displaystyle BB', F$ là trung điểm của $\displaystyle CC'$.

$\displaystyle O \in EF \Rightarrow O \in (CEF) \Rightarrow CO \subset \left( {CEF} \right)$

$\displaystyle A' \in CO \Rightarrow A' \in \left( {CEF} \right)$

Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành $\displaystyle CEA'F$.

Mặt phẳng $(CEA'F)$ chia khối hộp thành 2 phần: $ABCD.A'ECF$  ($\displaystyle V_1$) và $A'B'C'D'.CEA'F$ ($\displaystyle V_2$)

Qua $\displaystyle EF$ ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt $\displaystyle AA'$ ở $\displaystyle P$ và cắt $\displaystyle CC'$ ở $\displaystyle Q$.

Ta có:

$\displaystyle \begin{array}{l} {V_{ABCD.A'ECF}} = {V_{ABCD.EFP}} + {V_{A'.PEF}}\\ {V_{A'PEF}} = {V_{C.QEF}} \end{array}$

$\Rightarrow {V_{ABCD.A'ECF}} = {V_{ABCD.EFP}} + {V_{C.QEF}}$ $= {V_{ABCD.EPFQ}} = \dfrac{1}{2}V$

Do đó $\displaystyle {V_1} = {V_2} = \dfrac{1}{2}V \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 1$.

Chú ý: Có thể lí luận như sau: Giao điểm $\displaystyle O$ của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng $\displaystyle (CEF)$ chứa điểm $\displaystyle O$ nên chia hình hộp thành hai hình đối xứng với nhau qua điểm $\displaystyle O$. Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.

HocTot.Nam.Name.Vn