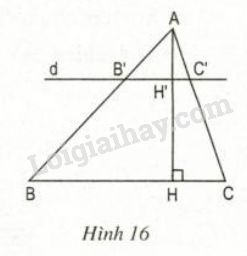
Bài 10 trang 63 SGK Toán 8 tập 2

LG a.

Chứng minh rằng:

\(\dfrac{AH'}{AH}= \dfrac{B'C'}{BC}\).

Phương pháp giải:

Áp dụng: Hệ quả của định lý TaLet.

Lời giải chi tiết:

Vì \(B'C' // BC\) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AB'}{AB}\)   (1) (theo hệ quả định lý TaLet)

Trong \(∆ABH\) có \(B'H' // BH\) \( \Rightarrow \dfrac{AH'}{AH} = \dfrac{AB'}{AB}\)  (2) (theo hệ quả định lý TaLet)

Từ (1) và (2) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AH'}{AH}\)

LG b.

Áp dụng: Cho biết \(AH' = \dfrac{1}{3} AH\) và diện tích \(∆ABC\) là \(67,5\) cm²

Tính diện tích \(∆AB'C'\).

Phương pháp giải:

Áp dụng: Hệ quả của định lý TaLet và công thức tính diện tích tam giác.

Lời giải chi tiết:

\(B'C' // BC\) mà \(AH ⊥ BC\) nên \(AH' ⊥ B'C'\) hay \(AH'\) là đường cao của \(∆AB'C'\).

 Giả thiết: \(AH' = \dfrac{1}{3} AH\).

Áp dụng kết quả câu a) ta có:

\(\dfrac{B'C'}{BC}= \dfrac{AH'}{AH} = \dfrac{1}{3}\) 

\(\Rightarrow  B'C' = \dfrac{1}{3} BC\)

\(\eqalign{
& {S_{AB'C'}} = {1 \over 2}AH'.B'C' \cr&\;\;\;\;\;\;\;\;\;\;\;= {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;= {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;= {1 \over 9}.{S_{ABC}}\cr&\;\;\;\;\;\;\;\;\;\;\; = {1 \over 9}.67,5 = 7,5\,\,c{m^2} \cr} \)

HocTot.Nam.Name.Vn