Bài 10 trang 27 SGK Hình học 12

LG a

a) Tính thể tích khối tứ diện \(A'BB'C\).

Phương pháp giải:

Gọi \(M\) là trung điểm của \(B'C'\). Chứng minh \(A'M \bot \left( {BCC'B'} \right)\). Áp dụng công thức \({V_{A'BB'C}} = \dfrac{1}{3}A'M.{S_{BB'C}}\).

Lời giải chi tiết:

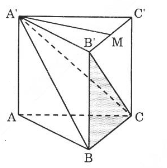
a) Ta tính thể tích hình chóp \(\displaystyle A'.BCB'\).

Gọi \(\displaystyle M\) là trung điểm của \(\displaystyle B'C'\), ta có: \(\displaystyle A'M \bot B'C'\)       (1)

Lăng trụ \(\displaystyle ABC.A'B'C'\) là lăng trụ đứng nên:

\(\displaystyle BB' \bot (A'B'C') \Rightarrow BB' \bot A'M\)           (2)

Từ (1) và (2) suy ra \(\displaystyle A'M \bot (BB'C')\) hay \(\displaystyle A'M\) là đường cao của hình chóp \(\displaystyle A'.BCB'\).

Ta có: \(\displaystyle A'M\) = \(\displaystyle {{a\sqrt 3 } \over 2};{S_{BB'C}} = {1 \over 2}{a^2}\)

\(\displaystyle \Rightarrow {V_{A'BB'C}} = {1 \over 3}.A'M.{S_{BB'C}}\) \( \Rightarrow {V_{A'BB'C}} =\displaystyle {{{a^3}\sqrt 3 } \over {12}}\)

Cách khác:

Ta chia khối lẳng trụ đã cho thành hình chóp \(A’.ABC, C.A’B’C’\) và \(C.A’BB’\)

Ta có: \({V_{A'.ABC}} = {V_{A'B'C'}} =\displaystyle \frac{1}{3}Sh\) trong đó \(S\) là diện tích đáy \(S = {\rm{ }}{S_{ABC\;}} = {\rm{ }}{S_{ABC}}\) và \(h\) là chiều cao của hình lăng trụ

Lại có: \({V_{ABC.ABC}}\; = {\rm{ }}S.h\)

Do đó, \({V_{C.A'B'B}} =\displaystyle Sh - \frac{1}{3}Sh - \frac{1}{3}Sh = \frac{1}{3}Sh\)

Trong đó, tam giác \(ABC\) là tam giác đều có độ dài cạnh bằng \(a\) nên \(\displaystyle {S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\)

Vì đây là hình lăng trụ đứng nên \(h = AA’ = BB’= CC’ = a.\)

Vậy thể tích hình chóp \(C.A’BB’\) là:

\({V_{C.A'B'B}} = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)

LG b

b) Mặt phẳng đi qua \(A'B'\) và trọng tâm tam giác \(ABC\), cắt \(AC\) và \(BC\) lần lượt tại \(E\) và \(F\). Tính thể tích hình chóp \(C.A'B'FE\).

Phương pháp giải:

Phân chia và lắp ghép các khối đa diện: \(V = {V_{B'.CEF}} + {V_{B'.A'EC}} = {V_1} + {V_2}\)

Lời giải chi tiết:

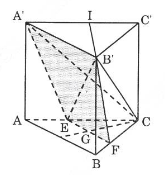
Thể tích hình chóp \(\displaystyle C.A'B'EF\) bằng tổng thể tích hai hình chóp:

- \(\displaystyle V_1\) là thể tích hình chóp đỉnh \(\displaystyle B'\), đáy là tam giác \(\displaystyle CEF\).

- \(\displaystyle V_2\) là thể tích hình chóp đỉnh \(\displaystyle B'\), đáy là tam giác \(\displaystyle A'EC\).

Do \(\displaystyle (ABC) // (A'B'C')\) nên dễ thấy \(\displaystyle EF // AB\). Ta cũng có: \(\displaystyle EF\) = \(\displaystyle {2 \over 3}a\)

Hình chóp \(\displaystyle B'.CEF\) có chiều cao \(\displaystyle BB' = a\) và diện tích đáy là: \(\displaystyle {S_{C{\rm{EF}}}}=\frac{1}{2}EF.CG = {1 \over 2}.{{2a} \over 3}.{2 \over 3}.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 9}\)

Từ đây ta có: \(\displaystyle {V_1} = {{{a^3}\sqrt 3 } \over {27}}\)

Do \(\displaystyle EC = {2 \over 3}AC\) nên \(\displaystyle {S_{A'BE}} = \frac{1}{2}A'A.EC = \frac{1}{2}.a.\frac{2}{3}a = \frac{{{a^2}}}{3}\)

Gọi \(\displaystyle I\) là trung điểm của \(\displaystyle A'C'\) ta có: \(\displaystyle \left\{ \begin{array}{l}B'I \bot A'C\\B'I \bot AA'\end{array} \right. \Rightarrow B'I \bot \left( {ACC'A'} \right) \Rightarrow B'I \bot \left( {A'EC} \right)\)

Hình chóp \(\displaystyle B'.A'EC\) có chiều cao là \(\displaystyle B'I\) bằng \(\displaystyle {{a\sqrt 3 } \over 2}\) nên \(\displaystyle {V_2} = \frac{1}{3}.B'I.{S_{A'EC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{{a^2}}}{3} = \frac{{{a^3}\sqrt 3 }}{{18}}\)

Vậy thể tích hình chóp \(\displaystyle C.A'B'FE\) là: \(\displaystyle V = V_1 + V_2\) = \(\displaystyle {{5{a^3}\sqrt 3 } \over {54}}\)

HocTot.Nam.Name.Vn