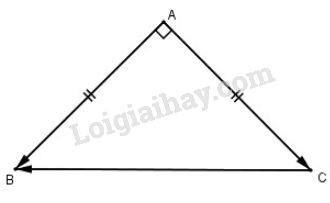
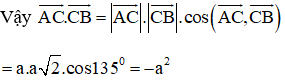Bài 1 trang 45 SGK Hình học 10Cho tam giác vuông cân ABC có AB = AC = a. Đề bài Cho tam giác vuông cân \(ABC\) có \(AB = AC = a\). Tính các tích vô hướng \(\vec{AB}.\vec{AC}\), \(\vec{AC}.\vec{CB}\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Cho hai vecto \(\overrightarrow a\) và \( \overrightarrow b \) đều khác vecto \( \overrightarrow 0. \) Khi đó tích vô hướng của vecto \(\overrightarrow a\) và \( \overrightarrow b \) được xác định bởi công thức sau: \[\overrightarrow a \overrightarrow {.b} = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\] Lời giải chi tiết
\(\vec{AB} ⊥\vec{AC}\Rightarrow \vec{AB}.\vec{AC} = 0\) \(\vec{AC}.\vec{CB} =(- \vec{CA}). \vec{CB}=- (\vec{CA}. \vec{CB})\) Ta có: \(CB= \sqrt{AB^2+AC^2}\)\(=\sqrt{a^2+a^2}=a\sqrt2\) Lại có \(\widehat{ACB} = 45^0\) vì \(\Delta ABC\) là tam giác vuông cân tại \(A.\) Vậy \(\vec{AC}.\vec{CB} = -(\vec{CA}. \vec{CB})\) \(= -|\vec{CA}|. |\vec{CB}|. \cos\widehat{ACB}\) \(= - CA. CB .\cos 45^0 \) \(= - a.a\sqrt 2 .{{\sqrt 2 } \over 2} = - {a^2}.\) Cách khác:
HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
