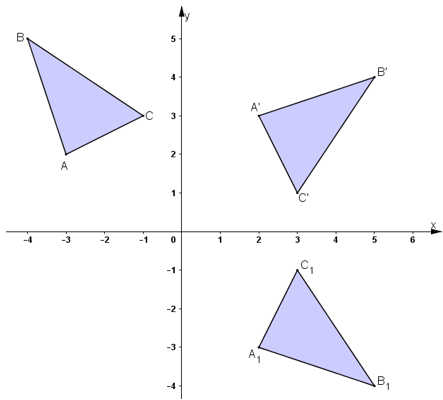
Bài 1 trang 23 SGK Hình học 11

LG a

Chứng minh rằng các điểm \(A'(2;3), B'(5;4)\) và \(C'(3;1)\) theo thứ tự là ảnh của \(A, B\) và \(C\) qua phép quay tâm \(O\) góc \( -90^{\circ}\)

Phương pháp giải:

Sử dụng định nghĩa phép quay 

\({Q_{\left( {O;\alpha } \right)}}\left( M \right) = M' \) \(\Leftrightarrow \left\{ \begin{array}{l}
OM' = OM\\
\left( {OM,OM'} \right) = \alpha
\end{array} \right.\)

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}
\overrightarrow {OA} = \left( { - 3;2} \right);\;\overrightarrow {OA'} = \left( {2;3} \right).\\
OA = \sqrt {{{( - 3)}^2} + {2^2}} = \sqrt {{2^2} + {3^2}} = OA'\\
\overrightarrow {OA} \,.\,\overrightarrow {OA'} = \left( { - 3} \right).2 + 2.3 = 0\\
\Rightarrow \widehat {AOA'} = {90^o}\\
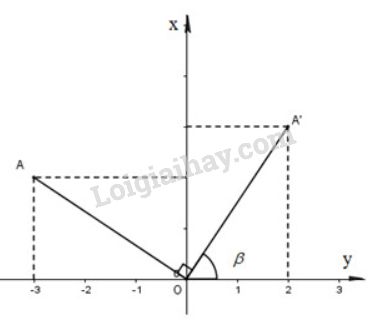
\Rightarrow \left( {OA;\;OA'} \right) = - \widehat {AOA'} = - {90^o}\\
\Rightarrow A' = {Q_{\left( {O; - {{90}^o}} \right)}}(A).
\end{array}\)

Tương tự ta cũng có \({Q_{\left( {O; - {{90}^0}} \right)}}\left( B \right) = B',\) \({Q_{\left( {O; - {{90}^0}} \right)}}\left( C \right) = C'\).

Chú ý:

Cách giải tham khảo (công thức mở rộng)

Sử dụng biểu thức tọa độ của phép quay: Ảnh của điểm \(M(x;y)\) qua phép quay tâm \(O\) góc quay \(\alpha\) là điểm \(M'(x';y')\) với \(x';y'\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)

(hình bên) 

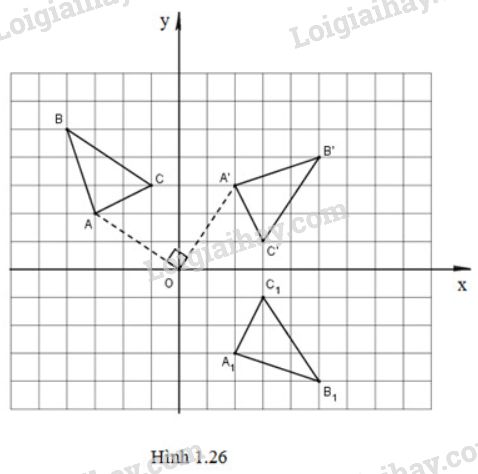
Phép quay tâm góc \(-90^0\) biến điểm \(M(x;y)\) thành điểm \(M'(x';y')\) với \(\left\{ \begin{array}{l}x' = x\cos \left( { - {{90}^0}} \right) - y\sin \left( { - {{90}^0}} \right) = y\\y' = x\sin \left( { - {{90}^0}} \right) + y\cos \left( { - {{90}^0}} \right) = - x\end{array} \right.\)

\( \Rightarrow A'\left( {2;3} \right);\,\,B'\left( {5;4} \right);\,\,C'\left( {3;1} \right)\) lần lượt là ảnh của \(A, B, C\) qua phép quay tâm \(O,\) góc quay \(-90^0\).

LG b

Gọi tam giác \({A_{1}}\)\({B_{1}}\)\({C_{1}}\) là ảnh của tam giác \(ABC\) qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm \(O\) góc \( -90^{\circ}\) và phép đối xứng qua trục \(Ox\). Tìm tọa độ các đỉnh của tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\) 

Phương pháp giải:

Thực hiện liên tiếp phép quay tâm \(O\) góc quay \(-90^0\) và phép đối xứng trục \(Ox\) trên mặt phẳng tọa độ \(Oxy.\)

Lời giải chi tiết:

(Hình 1.26)

Gọi tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\) là ảnh của tam giác \(A'B'C'\) qua phép đối xứng trục \(Ox\).

Khi đó,

\(\begin{array}{l}
{A_1} = {D_{Ox}}\left( {A'} \right) \Rightarrow {A_1}\left( {2; - 3} \right)\\
{B_1} = {D_{Ox}}\left( {B'} \right) \Rightarrow {B_1}\left( {5; - 4} \right)\\
{C_1} = {D_{Ox}}\left( {C'} \right) \Rightarrow {C_1}\left( {3; - 1} \right)
\end{array}\)

Vậy \({A_{1}}(2;-3), {B_{1}}^{}(5;-4), {C_{1}}^{}(3;-1).\)

HocTot.Nam.Name.Vn