Tuần 35: Ôn tập về tìm hai số khi biết tổng hoặc hiệu và tỉ số của hai số đó. Luyện tập chung (trang 60)Một khu đất hình chữ nhật có chu vi 130m, chiều dài hơn chiều rộng 17m. a) Tìm chiều dài và chiều rộng của khu đất. Bố mua ô tô và xe máy đồ chơi để thưởng cho Dũng hết 150 000 đồng.
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Viết số thích hợp vào ô trống:
Phương pháp giải: Tính ra nháp theo các bước bên dưới, sau đó ghi kết quả vào bảng : 1. Vẽ sơ đồ dựa vào tỉ số của hai số. 2. Tìm tổng (hoặc hiệu) số phần bằng nhau. 3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau (hoặc lấy hiệu chia cho hiệu số phần bằng nhau). 4. Tìm số bé (lấy giá trị 1 phần nhân với số phần của số bé) 5. Tìm số lớn (lấy tổng trừ đi số bé, lấy số bé cộng với hiệu, ...) Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết:
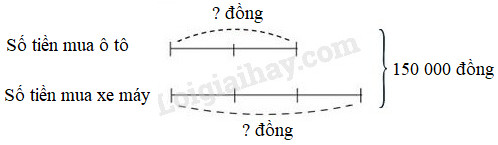
Câu 2 Tính: a) \(\dfrac{1}{2} + \dfrac{5}{3} - \dfrac{2}{7} = \ldots \) b) \(\dfrac{4}{5} + \dfrac{1}{3} \times \dfrac{1}{4} = \ldots \) c) \(\dfrac{9}{2} - \dfrac{1}{3}:\dfrac{1}{3} = \ldots \) d) \(\dfrac{7}{2} \times \dfrac{1}{3}:\dfrac{6}{5} = \ldots \) Phương pháp giải: - Biểu thức có các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước; thực hiện phép tính cộng, trừ sau. - Biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia thì ta thực hiện từ trái sang phải. Lời giải chi tiết: a) \(\dfrac{1}{2} + \dfrac{5}{3} - \dfrac{2}{7} = \dfrac{3}{6} + \dfrac{{10}}{6} - \dfrac{2}{7}\)\( = \dfrac{{13}}{6} - \dfrac{2}{7} = \dfrac{{91}}{{42}} - \dfrac{{12}}{{42}} = \dfrac{{79}}{{42}}\) b) \(\dfrac{4}{5} + \dfrac{1}{3} \times \dfrac{1}{4} = \dfrac{4}{5} + \dfrac{1}{{12}}\)\( = \dfrac{48}{60} + \dfrac{5}{60} = \dfrac{{53}}{{60}}\) c) \(\dfrac{9}{2} - \dfrac{1}{3}:\dfrac{1}{3} = \dfrac{9}{2} - \dfrac{1}{3} \times \dfrac{3}{1} \)\(= \dfrac{9}{2} - \dfrac{{3}}{3} = \dfrac{9}{2} - 1 = \dfrac{9}{2} - \dfrac{2}{2} = \dfrac{7}{2}\) d) \(\dfrac{7}{2} \times \dfrac{1}{3}:\dfrac{6}{5} = \dfrac{7}{{6}}:\dfrac{6}{5} \)\(= \dfrac{7}{{6}} \times \dfrac{5}{6} = \dfrac{{35}}{{36}}\) Câu 3 Một khu đất hình chữ nhật có chu vi 130m, chiều dài hơn chiều rộng 17m. a) Tìm chiều dài và chiều rộng của khu đất. b) Tính diện tích khu đất đó. Phương pháp giải: - Tính nửa chu vi ta lấy chu vi chia cho 2. - Nửa chu vi chính là tổng của chiều dài và chiều rộng. Tìm chiều dài và chiều rộng dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số đó: Số lớn = (Tổng + Hiệu) : 2; Số bé = (Tổng – Hiệu) : 2 - Tính diện tích khu đất hình chữ nhật ta lấy chiều dài nhân với chiều rộng. Lời giải chi tiết: Nửa chu vi khu đất đó là: 130 : 2 = 65 (m) Chiều dài khu đất đó là: (65 + 17) : 2 = 41 (m) Chiều rộng khu đất đó là: 41 – 17 = 24 (m) Diện tích khu đất đó là: 41 × 24 = 984 (m2) Đáp số: 984m2. Câu 4 Bố mua ô tô và xe máy đồ chơi để thưởng cho Dũng hết 150 000 đồng. Tìm giá tiền của ô tô và xe máy, biết rằng số tiền mua ô tô bằng \(\dfrac{2}{3}\) số tiền mua xe máy. Phương pháp giải: 1. Vẽ sơ đồ: coi số tiền mua ô tô (đóng vai trò số bé) gồm 2 phần bằng nhau thì số tiền mua xe máy (đóng vai trò số lớn) gồm3 phần như thế. 2. Tìm tổng số phần bằng nhau. 3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …). Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết: Ta có sơ đồ:
Theo sơ đồ, tổng số phần bằng nhau là: 2 + 3 = 5 (phần) Giá tiền của ô tô là: 150 000 : 5 × 2 = 60 000 (đồng) Giá tiền của xe máy là: 150 000 – 60 000 = 90 000 (đồng) Đáp số: Ô tô: 60 000 đồng; Xe máy: 90 000 đồng. Câu 5 Viết (theo mẫu):
Phương pháp giải: Khi đọc (hoặc viết) số tự nhiên, ta đọc (hoặc viết) từ trái sang phải, hay từ hàng cao tới hàng thấp. Lời giải chi tiết:
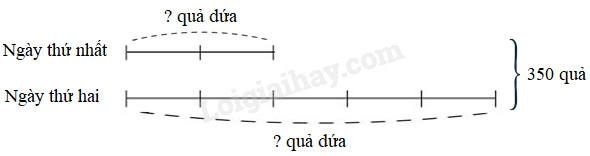
Câu 6 Điền dấu (>;<;=) thích hợp vào chỗ chấm: \(\dfrac{1}{4} \ldots \dfrac{2}{3}\) \(\dfrac{{15}}{9} \ldots \dfrac{{13}}{8}\) \(\dfrac{5}{11} \ldots \dfrac{{11}}{{23}}\) Phương pháp giải: Áp dụng quy tắc: Muốn so sánh hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng. Lời giải chi tiết: + Ta có: \(\dfrac{{1}}{4} = \dfrac{{1 \times 3}}{{4 \times 3}} = \dfrac{{3}}{{12}};\) \(\dfrac{{2}}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{{8}}{{12}}\). Mà \(\dfrac{{3}}{{12}} < \dfrac{{8}}{{12}}\). Vậy \(\dfrac{{1}}{4} < \dfrac{{2}}{3}\). + Ta có: \(\dfrac{{15}}{9} = \dfrac{{15 \times 8}}{{9 \times 8}} = \dfrac{{120}}{{72}};\) \(\dfrac{{13}}{8} = \dfrac{{13 \times 9}}{{8 \times 9}} = \dfrac{{117}}{{72}}\). Mà \(\dfrac{{120}}{{72}} > \dfrac{{117}}{{72}}\). Vậy \(\dfrac{{15}}{9} > \dfrac{{13}}{8}\). + Ta có: \(\dfrac{5}{11} = \dfrac{{5 \times 23}}{{11 \times 23}} = \dfrac{{115}}{{253}};\) \(\dfrac{{11}}{23} = \dfrac{{11 \times 11}}{{23 \times 11}} = \dfrac{{121}}{{153}}\). Mà \(\dfrac{{115}}{{253}} < \dfrac{{121}}{{153}}\). Vậy \(\dfrac{5}{11} < \dfrac{{11}}{{23}}\). Vậy ta có kết quả như sau: \(\dfrac{1}{4} < \dfrac{2}{3}\) \(\dfrac{{15}}{9} > \dfrac{{13}}{8}\) \(\dfrac{5}{11} < \dfrac{{11}}{{23}}\) Câu 7 Viết số thích hợp vào chỗ chấm: 3 tạ = …… kg 7 tạ 5kg = …… kg 5 tấn = …… kg 8 tấn 5kg = …… kg \(\dfrac{1}{4}\) tạ = …2… kg \(\dfrac{3}{5}\) tấn = …… kg Phương pháp giải: Áp dụng cách đổi: 1 tấn = 1000kg ; 1 tạ = 100kg. Lời giải chi tiết: 3 tạ = 300kg 7 tạ 5kg = 705kg 5 tấn = 5000kg 8 tấn 5kg = 8005kg \(\dfrac{1}{4}\) tạ = 25kg \(\dfrac{3}{5}\) tấn = 600kg Câu 8 Trong hai ngày chú Minh bán được 350 quả dứa, biết rằng số quả dứa bán được của ngày thứ nhất bằng \(\dfrac{2}{5}\) số quả dứa bán được của ngày thứ hai. Hỏi mỗi ngày chú Minh bán được bao nhiêu quả dứa? Phương pháp giải: 1. Vẽ sơ đồ: coi số quả dứa bán được của ngày thứ nhất (đóng vai trò số bé) gồm 2 phần bằng nhau thì số quả dứa bán được của ngày thứ hai (đóng vai trò số lớn) gồm 5 phần như thế. 2. Tìm tổng số phần bằng nhau. 3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau. 4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé). 5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …). Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau. Lời giải chi tiết: Ta có sơ đồ:
Theo sơ đồ, tổng số phần bằng nhau là: 2 + 5 = 7 (phần) Ngày thứ nhất chú Minh bán được số quả dứa là: 350 : 7 × 2 = 100 (quả) Ngày thứ hai chú Minh bán được số quả dứa là: 350 – 100 = 250 (quả) Đáp số: Ngày thứ nhất: 100 quả; Ngày thứ hai: 250 quả. Vui học Viết số thích hợp vào chỗ chấm: Minh được mẹ cho 200 000 đồng. Minh dùng \(\dfrac{2}{3}\) số tiền để mua sách và dùng \(\dfrac{1}{4}\) số tiền còn lại để mua đồ dùng học tập. a) Sau khi mua sách và đồ dùng học tập Minh còn lại …… đồng. b) Nếu giá bán mỗi cuốn sách là 25 000 đồng thì Minh đã mua được …… cuốn sách.
Phương pháp giải: - Tìm số tiền Minh dùng để mua sách ta lấy số tiền ban đầu mẹ cho Minh nhân với \(\dfrac{2}{3}\), hay lấy \(300\,\,000\) đồng nhân với \(\dfrac{2}{3}\). - Tìm số tiền còn lại sau khi mua sách ta lấy số tiền ban đầu mẹ cho Minh trừ đi số tiền dùng để mua sách. - Tìm số tiền mua đồ dùng học tập ta lấy số tiền còn lại sau khi mua sách nhân với \(\dfrac{1}{4}\). - Tìm số tiền còn lại sau khi mua sách và đồ dùng học tập ta lấy số tiền ban đầu mẹ cho Minh trừ đi tổng số tiền mua sách và đồ dùng học tập hoặc lấy số tiền còn lại sau khi mua sách trừ đi số tiền mua đồ dùng học tập. - Tìm số cuốn sách Minh đã mua được ta lấy số tiền Minh dùng để mua sách chia cho giá bán của mỗi cuốn sách. Lời giải chi tiết: a) Minh mua sách hết số tiền là: \(300\,\,000 \times \dfrac{2}{3} = 200\;000\) (đồng) Sau khi mua sách Minh còn lại số tiền là: \(300\;000 - 200\;000 = 100\;000\) (đồng) Minh mua đồ dùng học tập hết số tiền là: \(100\;000 \times \dfrac{1}{4} = 25\;000\) (đồng) Sau khi mua sách và đồ dùng học tập Minh còn lại số tiền là: \(300\;000 - (200\;000 + 25\;000) = 75\;000\) (đồng) b) Minh đã mua được số cuốn sách là: \(200\;000:25\;000 = 8\) (cuốn) Đáp số: a) \(75\;000\) đồng; b) \(8\) cuốn sách.
|