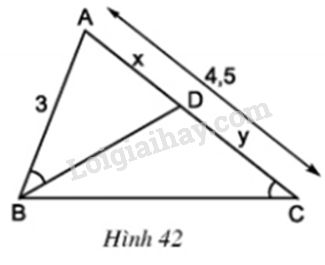
Trả lời câu hỏi 2 Bài 7 trang 79 SGK Toán 8 Tập 2

LG a

Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?

Phương pháp giải:

Áp dụng: 

- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. 

Lời giải chi tiết:

Trong hình vẽ có $3$ tam giác: $ΔABD, ΔCBD, ΔABC$.

$ΔABD$ và $ΔACB$ có

$\widehat B = \widehat C$

$\widehat A$  chung

$⇒ ΔABD  ∽ ΔACB$ (g.g)

LG b

Hãy tính các độ dài $x$ và $y$ ($AD = x, DC = y$).

Phương pháp giải:

Áp dụng: Tính chất hai tam giác đồng dạng

Lời giải chi tiết:

Vì $ΔABD  ∽ ΔACB$

$\eqalign{&  \Rightarrow {{AB} \over {AD}} = {{AC} \over {AB}}\cr}$ ( cặp cạnh tương ứng tỉ lệ)

$\Rightarrow {3 \over {AD}} = {{4,5} \over 3}\\ \Rightarrow AD = x = {{3.3} \over {4,5}} = 2 cm$

$⇒ y = 4,5 - 2 = 2,5 cm$

LG c

Cho biết thêm $BD$ là tia phân giác của góc $B$. Hãy tính độ dài các đoạn thẳng $BC$ và $BD$.

Phương pháp giải:

Áp dụng: Tính chất đường phân giác trong tam giác.

Lời giải chi tiết:

$BD$ là tia phân giác của góc $B$

$\eqalign{ &  \Rightarrow {{AB} \over {BC}} = {x \over y} \cr}$ ( Tính chất đường phân giác của tam giác)

$\Rightarrow {3 \over {BC}} = {2 \over {2,5}}\\  \Rightarrow BC = {{3.2,5} \over 2} = 3,75 cm$

Ta có: 

$\Delta ABD  ∽\Delta ACB \Rightarrow {{AB} \over {BD}} = {{AC} \over {BC}}$(cặp cạnh tương ứng tỉ lệ)

$\Rightarrow {3 \over {BD}} = {{4,5} \over {3,75}}\\ \Rightarrow BD = {{3.3,75} \over {4,5}} = 2,5 cm$