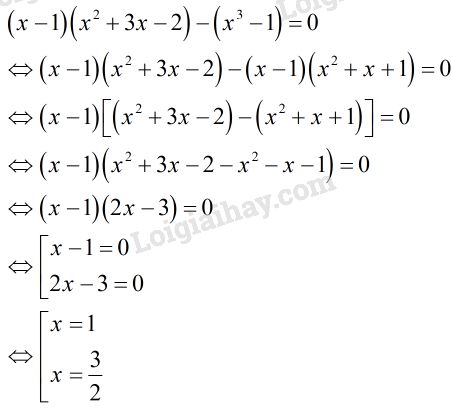Trả lời câu hỏi 3 Bài 4 trang 16 SGK Toán 8 Tập 2Giải phương trình: Đề bài Giải phương trình: (x−1)(x2+3x−2)−(x3−1)=0 Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Sử dụng hằng đẳng thức số 7: A3−B3=(A−B)(A2+AB+B2) - Phân tích: x3−1=(x−1)(x2+x+1) Từ đó tìm được nhân tử chung là (x−1), đưa phương trình về dạng phương trình tích. - Giải phương trình tích ta áp dụng công thức: A(x).B(x)=0 ⇔A(x)=0 hoặc B(x)=0 Lời giải chi tiết
Vậy tập nghiệm của phương trình là S={1;32} HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
