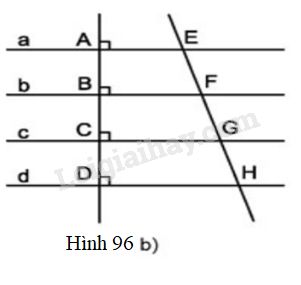
Trả lời câu hỏi 4 Bài 10 trang 102 SGK Toán 8 Tập 1

LG a.

Nếu các đường thẳng \(a, b, c, d\) song song cách đều thì \(EF = FG = GH.\)

Phương pháp giải:

Áp dụng đinh lí:

Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai cạnh đáy của hình thang thì đi qua trung điểm của cạnh bên thứ hai.

Lời giải chi tiết:

Các đường thẳng \(a, b, c, d\) song song cách đều \(⇒ AB = BC = CD\)

\(⇒ B\) là trung điểm của \(AC\); \(C\) là trung điểm của \(BD\).

- Hình thang \(AEGC\) (vì \(AE // GC\)) có \(B\) là trung điểm của \(AC\) và \(BF\) song song với hai cạnh đáy

\(⇒ F\) là trung điểm của \(EG\) (định lí đường trung bình của hình thang)

\(⇒ EF = FG\)

- Hình thang \(BFHD\) (vì \(BF// DH\)) có \(C\) là trung điểm của \(BD\) và \(CG\) song song với hai cạnh đáy

\(⇒ G\) là trung điểm của \(FH\) (định lí đường trung bình của hình thang)

\(⇒ GH = FG\)

Vậy \(EF = FG = GH\). 

LG b.

Nếu \(EF = FG = GH\) thì các đường thẳng \(a, b, c, d\) song song cách đều.

Phương pháp giải:

Áp dụng đinh lí:

Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai cạnh đáy của hình thang thì đi qua trung điểm của cạnh bên thứ hai.

Lời giải chi tiết:

Có Các đường thẳng \(a, b, c, d\) song song và \(EF = FG = GH\).

\(EF=FG\) nên \(F\) là trung điểm của \(EG\) 

\(GH=FG\) nên \(G\) là trung điểm của \(FH\)

- Hình thang \(AEGC\) (vì \(AE // GC\)) có \(F\) là trung điểm của \(EG\) và \(BF\) song song hai cạnh đáy.

\(⇒ B\) là trung điểm của \(AC\) (định lí đường trung bình của hình thang).

\( \Rightarrow AB = BC\).

- Hình thang \(BFHD\) (vì \(BF// DH\)) có \(G\) là trung điểm của \(FH\) và \(CG\) song song với hai cạnh đáy

\(⇒ C\) là trung điểm của \(BD\) (định lí đường trung bình của hình thang)

\(⇒ BC = CD\)

Vậy \(AB = BC = CD\).

Hay \(a,b,c,d\) song song cách đều.

HocTot.Nam.Name.Vn