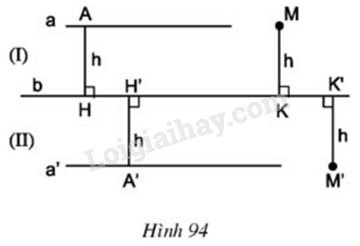
Trả lời câu hỏi 2 Bài 10 trang 101 SGK Toán 8 Tập 1

Đề bài

Cho đường thẳng \(b\). Gọi \(a\) và \(a’\) là hai đường thẳng song song với đường thẳng \(b\) và cùng cách đường thẳng \(b\) một khoảng bằng \(h \) (h.\(94\)), (I) và (II) là các nửa mặt phẳng bờ \(b.\) Gọi \(M, M’\) là các điểm cách đường thẳng \(b\) một khoảng bằng \(h\), trong đó \(M\) thuộc nửa mặt phẳng (I), \(M’\) thuộc nửa mặt phẳng (II). Chứng minh rằng \(M ∈ a, M’ ∈ a’.\)

Lời giải chi tiết

- Tứ giác \(AMKH\) có \(AH = MK = h\) và \(AH // MK\) (vì cùng \(⊥ b\))

\(⇒\) Tứ giác \(AMKH\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\(⇒ AM // HK\) (tính chất hình bình hành).

Mà \(a // b\) (giả thiết) \(⇒ a // HK\)

Do đó \(AM\) trùng với \(a\) (theo tiên đề ơclit) hay \(M ∈ a\).

- Tứ giác \(A'M'K'H'\) có \(A'H'=M'K'=h\) và \(A'H'//M'K'\) (vì cùng \( \bot b\))

\(⇒\) Tứ giác \(A'M'K'H'\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow A'M'//H'K'\) (tính chất hình bình hành).

Mà \(a'//b\) (giả thiết) \(⇒ a' // H'K'\)

Do đó \(A'M'\) trùng với \(a'\) (theo tiên đề ơclit) hay \(M’ ∈ a’\).

HocTot.Nam.Name.Vn