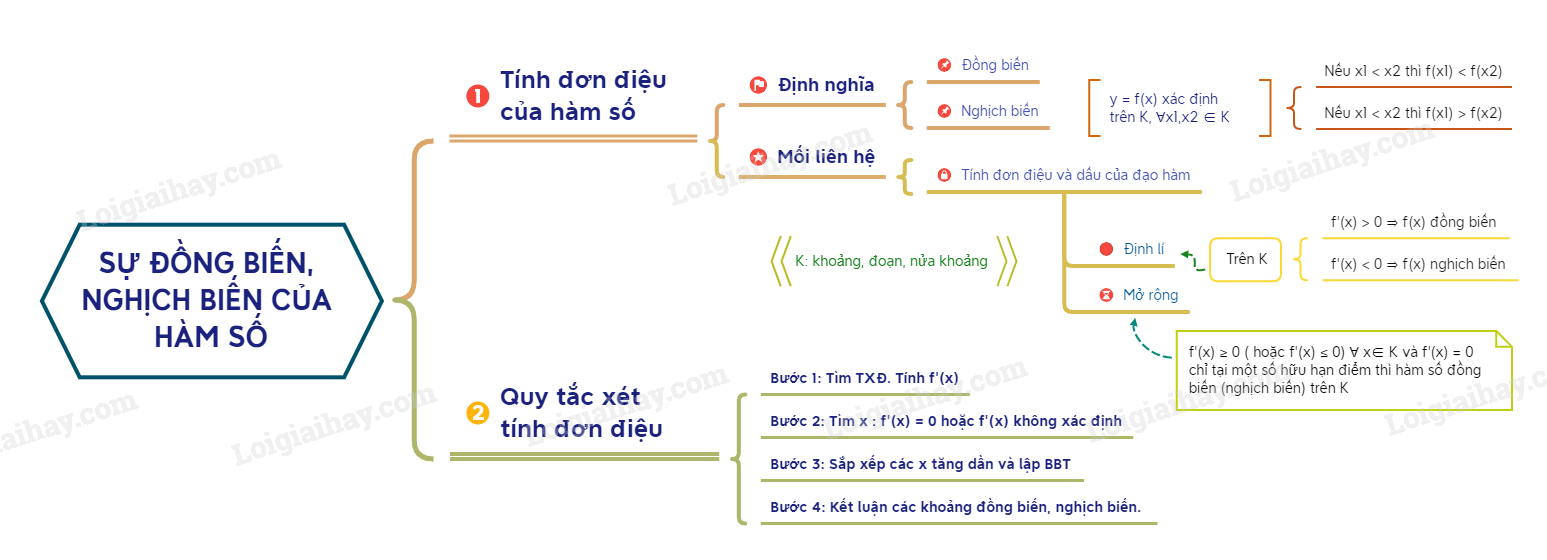
Tính đơn điệu của hàm sốTính đơn điệu của hàm số, khảo sát sự biến thiên, tính đơn điệu của hàm số, điều kiện để hàm số đồng biến - nghịch biến 1. Định nghĩa Hàm số f xác định trên K. Với mọi x1,x2 thuộc K mà x1>x2 +) nếu f(x1)>f(x2) thì f tăng trên K +) nếu f(x1)<f(x2) thì f giảm trên K. Chú ý: - Hàm số tăng hoặc giảm trên K được gọi chung là hàm số đơn điệu trên K. - K có thể là một khoảng, một đoạn hoặc một nửa khoảng. 2. Điểu kiện cần đế hàm số đơn điệu Cho hàm số f có đạo hàm trên khoảng K - Nếu f tăng trên K thì f′(x)>0, với mọi x thuộc K. - Nếu f giảm trên K thì f′(x)<0, với mọi x thuộc K. 3. Điều kiện đủ để hàm số đơn điệu Cho hàm sổ f có đạo hàm trên khoảng K - Nếu f′(x)>0 với mọi x thuộc K thì f tăng trên K. - Nếu f′(x)<0 với mọi x thuộc K thì f giảim trên K. Chú ý: Nếu f′(x)≥0 ∀x∈K (hoặc f′(x)≤0, ∀x∈K) và f′(x)=0 chỉ tại một số hữu hạn điểm thuộc K thì hàm số f tăng (hoặc giảm) trên K.
HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|