Phương pháp giải một số dạng bài tập về sóng cơ và sự truyền sóng cơTổng hợp cách giải một số dạng bài tập về sóng cơ và sự truyền sóng cơ thường gặp I. Phương pháp giải bài tập sóng cơ - Các đại lượng đặc trưng cơ bản của sóng cơ học Phương pháp: - Chu kỳ \(\left( T \right)\) , vận tốc \(\left( v \right)\) , tần số \(\left( f \right)\) , bước sóng \((\lambda )\) liên hệ với nhau : \(f = \frac{1}{T};\lambda = vT = \frac{v}{f};v = \frac{{\Delta s}}{{\Delta t}}\) với \(\Delta s\) là quãng đường sóng truyền trong thời gian \(\Delta t\). - Quan sát hình ảnh sóng có n ngọn sóng liên tiếp thì có n - 1 bước sóng. Hoặc quan sát thấy từ ngọn sóng thứ n đến ngọn sóng thứ m (m > n) có chiều dài l thì bước sóng: \(\lambda = \frac{l}{{m - n}}\) - Số lần nhô lên trên mặt nước là N trong khoảng thời gian t giây thì \(T = \frac{t}{{N - 1}}\) 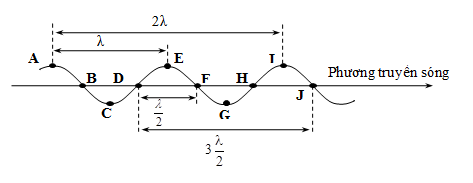 - Độ lệch pha giữa hai điểm cách nguồn một khoảng xM, xN: 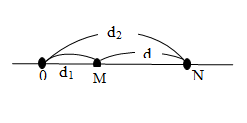 \(\Delta {\varphi _{MN}} = \omega \frac{{{x_N} - {x_M}}}{v} = 2\pi \frac{{{x_N} - {x_M}}}{\lambda } = 2\pi \frac{d}{\lambda }\) trong đó: \({x_N} - {x_M} = d\)
\(\Delta {\varphi _{MN}} = 2k\pi < = > 2\pi \frac{d}{\lambda } = 2k\pi < = > d = k\lambda \). \(({\rm{ }}k \in Z{\rm{ }})\)
\(\Delta {\varphi _{MN}} = (2k + 1)\pi < = > 2\pi \frac{d}{\lambda } = (2k + 1)\pi < = > d = (2k + 1)\frac{\lambda }{2}\). \(({\rm{ }}k \in Z{\rm{ }})\)
\(\Delta {\varphi _{MN}} = (2k + 1)\frac{\pi }{2} < = > 2\pi \frac{d}{\lambda } = (2k + 1)\frac{\pi }{2} < = > d = (2k + 1)\frac{\lambda }{4}\). \(({\rm{ }}k \in Z{\rm{ }})\) Đơn vị của \(x,{\rm{ }}{x_1},{\rm{ }}{x_2},d,\lambda ,v\) phải tương ứng với nhau. Bài tập ví dụ: Một người ngồi ở bờ biển trông thấy có 10 ngọn sóng qua mặt trong 36 giây, khoảng cách giữa hai ngọn sóng liên tiếp là 10m. Tính tần số sóng biển và vận tốc truyền sóng biển. Hướng dẫn giải Xét tại một điểm có 10 ngọn sóng truyền qua trong 36 giây => 9T = 36 => T = 36/9 = 4s Khoảng cách giữa hai ngọn sóng liên tiếp bằng một bước sóng => \(\lambda = 10m\) Tần số sóng biển: \(f = \frac{1}{T} = \frac{1}{4} = 0,25Hz\) Vận tốc truyền sóng: \(v = \frac{\lambda }{T} = \frac{{10}}{4} = 2,5m/s\) II. Phương pháp giải bài tập sóng cơ - Phương trình sóng cơ1. Xác định biên độ, li độ, vận tốc dao động sóng cơ Phương pháp: - Cách 1: Thay vào phương trình sóng \(\begin{array}{l}{u_M} = Ac{\rm{os}}\omega \left( {t - \dfrac{x}{v}} \right) = Ac{\rm{os}}\left( {\omega t - \dfrac{{2\pi x}}{\lambda }} \right)\\v = x' = - A\omega \sin \left( {\omega t - \dfrac{{2\pi x}}{\lambda }} \right)\end{array}\) - Cách 2: Dùng vòng tròn lượng giác. DĐĐH được xem là hình chiếu của một chất điểm chuyển động tròn đều lên một trục nằm trong mặt phẳng quỹ đạo. Với: \(A = R;\omega = \dfrac{v}{R}\) 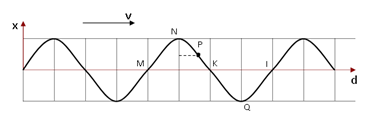 (VD: điểm N) xác định trạng thái dao động của điểm khác ta tiến hành như sau: Nếu điểm đó sau N ( theo phương truyền sóng), ví dụ là điểm K, khi đó K sẽ trễ pha hơn N góc \(\Delta \varphi = 2\pi \dfrac{{\Delta d}}{\lambda }\) với \(\Delta d = {\rm{ }}NK\). Từ N quay góc \(\Delta \phi \) theo chiều kim đồng hồ ta sẽ xác định được trạng thái của K. 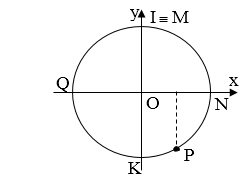 Nếu điểm cần tìm trước N (theo phương truyền sóng), ví dụ là M, ta cũng tính \(\Delta \varphi \) theo công thức trên với \(\Delta d = MN\) , từ N quay theo chiểu ngược kim đồng hồ góc \(\Delta \varphi \) ta được M 2. Viết phương trình dao động tại một điểm trên phương truyền sóng Phương pháp: Phương trình tại nguồn: \({u_0} = Ac{\rm{os}}\omega {\rm{t}}\) PT sóng có dạng: \({u_M} = Ac{\rm{os}}\omega \left( {t - \dfrac{x}{v}} \right) = Ac{\rm{os}}\left( {\omega t - \dfrac{{2\pi x}}{\lambda }} \right)\) - Bước 1: Xác định A, ω, φ: dựa theo dữ kiện đề bài cho. pha ban đầu của sóng tại M: \({\varphi _M} = \varphi - 2\pi \dfrac{{\overline {OM} }}{\lambda } = \varphi - 2\pi \dfrac{x}{\lambda }\) - Bước 2: Viết phương trình sóng
Bài tập ví dụ: Một sóng ngang truyền từ M đến O rồi đến N trên cùng một phương truyền song với vận tốc v = 18 m/s. Biết MN = 3 m và MO = ON, phương trình sóng tại O là \({u_O} = 5\cos \left( {4\pi t - \frac{\pi }{6}} \right)\left( {cm} \right)\). Viết phương trình sóng tại M và N. Hướng dẫn giải Ta có: \(\omega = 4\pi \Rightarrow T = \frac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) Bước sóng: \(\lambda = v.T = 18.0,5 = 9m\) Vì M ở trước O theo chiều truyền sóng nên: \({u_M} = 5\cos \left( {4\pi t - \frac{\pi }{6} + \frac{{2\pi .MO}}{\lambda }} \right) \\= 5\cos \left( {4\pi t - \frac{\pi }{6} + \frac{\pi }{3}} \right)\\ = 5\cos \left( {4\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)\) N ở sau O nên: \({u_N} = 5\cos \left( {4\pi t - \frac{\pi }{6} - \frac{{2\pi .NO}}{\lambda }} \right) \\= 5\cos \left( {4\pi t - \frac{\pi }{6} - \frac{\pi }{3}} \right) \\= 5\cos \left( {4\pi t - \frac{\pi }{2}} \right)\left( {cm} \right)\) III. Giải bài tập sóng cơ - Đồ thị sóng cơ học 1. Biên độ, chu kì sóng và bước sóng 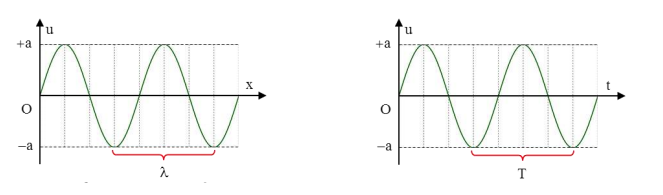 2. Trạng thái chuyển động của các phần tử môi trường Theo phương truyền sóng, các phần tử môi trường ở trước một đỉnh sóng gần nhất sẽ chuyển động đi xuống, các phần tử môi trường ở sau đỉnh gần nhất sẽ chuyển động đi lên. 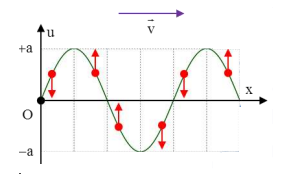
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|





















