Phương pháp giải một số dạng bài tập về mạch dao độngTổng hợp cách giải một số dạng bài tập về mạch dao động thường gặp 1. Dạng 1: Xác định chu kì, tần số của mạch dao động - Tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}{\rm{ }} \to T = 2\pi \sqrt {LC} ;{\rm{ }}f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
- Bài toán ghép tụ điện nối tiếp và song song Mạch gồm L và C1 có tần số f1 - Mạch gồm L và C2 có tần số f2 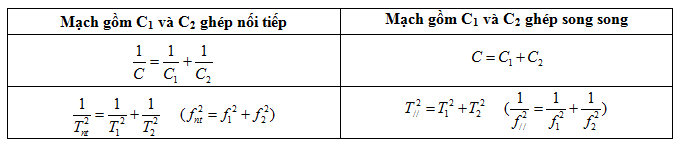 - Bài toán ghép cuộn cảm nối tiếp và song song Mạch gồm L1 và C có tần số f1 - Mạch gồm L2 và C có tần số f2 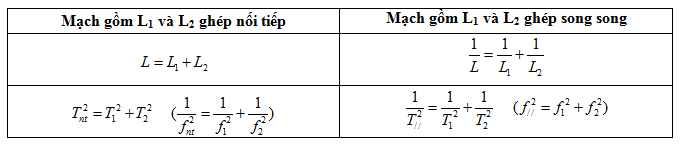
Ví dụ: Một mạch dao động gồm cuộn dây L và tụ điện C. Nếu dùng tụ \({C_1}\) thì tần số dao động riêng của mạch là 60kHz, nếu dùng tụ \({C_2}\) thì tần số dao động riêng là 80kHz. Hỏi tần số dao động riêng của mạch là bao nhiêu nếu: a) Hai tụ \({C_1}\) và \({C_2}\) mắc song song b) Hai tụ \({C_1}\) và \({C_2}\) mắc nối tiếp Hướng dẫn giải a) \({C_1}//{C_2}\) => \(\frac{1}{{{f^2}}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} = \frac{1}{{{{60}^2}}} + \frac{1}{{{{80}^2}}} \Rightarrow f = 48kHz\) b) \({C_1}nt{C_2}\) => \({f^2} = f_1^2 + f_2^2 = {60^2} + {80^2} \Rightarrow f = 100kHz\) 2. Dạng 2: Xác định I0, Q0, U0, u, i - Từ phương trình dao động: \(q = {Q_0}cos\left( {\omega t + \varphi } \right),i = q' = - \omega {Q_0}sin(\omega t + \varphi ) = {I_0}cos(\omega t + \varphi + \dfrac{\pi }{2})\) \(u = \dfrac{q}{C} = \dfrac{{{Q_0}}}{C}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{) = }}{{\rm{U}}_0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{)}}\) => Mối liên hệ giữa các đại lượng: \({I_0} = \omega {Q_0} = \dfrac{{{Q_0}}}{{\sqrt {LC} }}\) , \({U_0} = \dfrac{{{Q_0}}}{C} = \dfrac{{{I_0}}}{{\omega C}} = \omega L{I_0} = {I_0}\sqrt {\dfrac{L}{C}} \) - Điện áp tức thời:
- Dòng điện tức thời:
- Điện tích tức thời:
Điện áp và cường độ dòng điện hiệu dụng: \(U = \dfrac{{{U_0}}}{{\sqrt 2 }};I = \dfrac{{{I_0}}}{{\sqrt 2 }}\) 3. Dạng 3. Năng lượng của mạch dao động LC a. Phương pháp - Năng lượng điện trường tập trung ở trong tụ điện: \({W_d} = \dfrac{1}{2}C{u^2} = \dfrac{1}{2}qu = \dfrac{{{q^2}}}{{2C}} = \dfrac{{Q_0^2}}{{2C}}{\rm{co}}{{\rm{s}}^2}(\omega t + \varphi )\) - Năng lượng từ trường tập trung trong cuộn cảm: \({W_t} = \dfrac{1}{2}L{i^2} = \dfrac{{Q_0^2}}{{2C}}{\sin ^2}\left( {\omega t + \varphi } \right)\) - Trong quá trình dao động của mạch, năng lượng từ và năng lượng điện trường luôn chuyển hóa cho nhau, nhưng tổng năng lượng điện từ là không đổi. - Năng lượng điện từ: \(W = {W_d} + {W_t} = \dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2} = \dfrac{1}{2}CU_0^2 = \dfrac{{Q_0^2}}{{2C}} = \dfrac{1}{2}LI_0^2\) - Vị trí năng lượng điện trường gấp $n$ lần năng từ điện trường: \(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}i = \pm \dfrac{{{I_0}}}{{\sqrt {n + 1} }}\\u = \pm {U_0}\sqrt {\dfrac{n}{{n + 1}}} \\q = \pm {Q_0}\sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\) - Mạch có cuộn dây không thuần cảm (r≠0): Công suất tỏa nhiệt trên r hay công suất cần phải cung câp thêm cho mạch để duy trì dao động: \(P = {I^2}r = \dfrac{{I_0^2}}{2}r\)
b. Ví dụ
Hướng dẫn: Sử dụng công thức tính năng lượng của mạch dao động: \(W = \dfrac{1}{2}CU_0^2\) Thay U0=60 V, C=1μF vào, ta được: \(W = \dfrac{1}{2}CU_0^2 = \dfrac{1}{2}{10^{ - 6}}{60^2} = {1,8.10^{ - 3}}(J)\)
Hướng dẫn: Sử dụng công thức tính năng lượng của mạch dao động: \(W = {W_d} + {W_t}\) Ta có: \(W = {W_d} + {W_t} = \dfrac{1}{2}LI_0^2 \to {W_d} = W - {W_t} = \dfrac{1}{2}LI_0^2 - \dfrac{1}{2}L{i^2} = \dfrac{L}{2}(I_0^2 - {i^2}) = \dfrac{{{{5.10}^{ - 6}}}}{2}({2^2} - {1^2}) = {7,5.10^{ - 6}}(J)\) 4. Dạng 4. Viết phương trình dao động Ta có: - Phương trình điện tích trên hai bản tụ điện: \(q{\rm{ }} = {\rm{ }}{Q_0}cos\left( {\omega t + {\varphi _q}} \right)\) - Phương trình điện áp giữa hai bản tụ điện: \(u = \frac{{{Q_0}}}{C}cos\left( {\omega t + {\varphi _u}} \right){\rm{ }} = {U_0}cos\left( {\omega t + {\varphi _u}} \right)\) - Phương trình điện áp dòng điện chạy trong mạch: \(i = q' = - {Q_0}\omega sin{\varphi _q} = {I_0}cos\left( {\omega t + {\varphi _i}} \right)\) Trong đó:
Các bước viết phương trình dao động:
tại t = 0: \(\left\{ \begin{array}{l}q = {Q_0}{\rm{cos}}\varphi \\i = - {I_0}\omega {\rm{sin}}\varphi \\u = {U_0}{\rm{cos}}\varphi \end{array} \right. \to \varphi \) (Ta chỉ cần 2 dữ kiện q và i hoặc i và u để xác định φ)
Lưu ý: Các bước có thể đổi vị trí cho nhau Ví dụ:
Hướng dẫn: Cường độ dòng điện cực đại: \({I_0} = {Q_0}\omega = {2,5.10^{ - 6}}{.2.10^3}\pi = {5.10^{ - 3}}\pi A = 5\pi {\rm{ }}mA\) \({\varphi _i} = {\varphi _q} + \frac{\pi }{2} = \frac{\pi }{3} + \frac{\pi }{2} = \frac{{5\pi }}{6}\) \( \to i = 5\pi c{\rm{os(2}}{\rm{.1}}{{\rm{0}}^3}\pi t + \frac{{5\pi }}{6}){\rm{ mA}}\)
Điện tích cực đại giữa hai bản tụ điện: \({Q_0} = \frac{{{I_0}}}{\omega } = \frac{{{{20.10}^{ - 3}}}}{{{{10}^7}}} = {2.10^{ - 9}}C = 2{\rm{ }}nC\) Tại \(t = 0,{\rm{ }}i = {I_0}cos{\varphi _i} = {I_0} = > {\rm{ }}{\varphi _i} = {\rm{ }}0\) =>\({\varphi _u} = {\varphi _i} - \frac{\pi }{2} = - \frac{\pi }{2}\)\(\) \( \to q = 2c{\rm{os(1}}{{\rm{0}}^7}t - \frac{\pi }{2}){\rm{ }}nC\) 5. Dạng 5. Thời điểm điện tích trện tụ biến thiên từ q1 đến q2 (Tương tự bài toán xác định thời gian vật chuyển động từ vị trí có li độ x1 đến vị trí có li độ x2 trong dao động điều hòa) Phương pháp: Sử dụng vòng tròn lượng giác và công thức \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)
|













