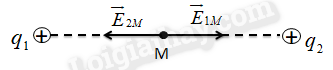
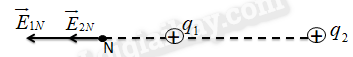Phương pháp giải một số dạng bài tập về điện trường – cường độ điện trường

Dạng 1: Xác định cường độ điện trường do điện tích gây ra tại một điểm 

Cường độ điện trường do điện tích Q gây ra có:

- Điểm đặt: tại điểm ta xét

- Phương: Trùng với đường thẳng nối điện tích Q và điểm ta xét

- Chiều:

+ Hướng ra xa Q nếu Q > 0

+ Hướng về Q nếu Q < 0

- Độ lớn: \(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}}\)

Bài tập ví dụ: Xác định vecto cường độ điện trường tại điểm M trong không khí cách điện tích điểm Q = 10^-16C một khoảng 30 cm.

Hướng dẫn giải

Ta có: Q > 0 nên vecto E có gốc đặt tại M, chiều hương ra xa điện tích Q.

Độ lớn: \(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}} = {9.10^9}\frac{{{{10}^{ - 6}}}}{{1.{{\left( {{{30.10}^{ - 2}}} \right)}^2}}} = {10^5}V/m\)

Dạng 2: Xác định cường độ điện trường tổng hợp do nhiều điện tích gây ra tại một điểm

- Áp dụng nguyên lý chồng chất điện trường: \(\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  + \overrightarrow {{E_3}}  + ... + \overrightarrow {{E_n}} \)

- Biểu diễn \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} ,...,\overrightarrow {{E_n}} \), xác định phương, chiều, độ lớn của từng vecto cường độ điện trường do từng điện tích gây ra.

- Vẽ vecto cường độ điện trường tổng hợp theo quy tắc hình bình hành.

- Xác định độ lớn của cường độ điện trường tổng hợp dựa vào hình vẽ.

* Các trường hợp đặc biệt:

+ \(\overrightarrow {{E_1}}  \uparrow  \uparrow \overrightarrow {{E_2}}  \Rightarrow E = {E_1} + {E_2}\)

+ \(\overrightarrow {{E_1}}  \uparrow  \downarrow \overrightarrow {{E_2}}  \Rightarrow E = \left| {{E_1} - {E_2}} \right|\)

+ \(\overrightarrow {{E_1}}  \bot \overrightarrow {{E_2}}  \Rightarrow E = \sqrt {{E_1}^2 + {E_2}^2} \)

+ \((\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ) = \alpha  \Rightarrow E = \sqrt {{E_1}^2 + {E_2}^2 + 2{{\rm{E}}_1}{E_2}\cos \alpha } \)

Bài tập ví dụ: Tại hai điểm A và B cách nhau 10 cm trong không khí có đặt hai điện tích \({q_1} = {q_2} = {16.10^{ - 8}}C\). Xác định cường độ điện trường do hai điện tích điểm này gây ra tại:

a) M với MA = MB = 5 cm

b) N với NA = 5 cm, NB = 15 cm

Hướng dẫn giải

a)

MA = MB = 5 cm, AB = 10 cm => M là trung điểm của AB.

Ta biểu diễn các vecto cường độ điện trường do hai điện tích gây ra tại điểm M như hình vẽ. 

Vecto cường độ điện trường tại M là tổng hợp hai vecto \(\overrightarrow {{E_{1M}}} ,\overrightarrow {{E_{2M}}} \)

Suy ra \(\overrightarrow E  = \overrightarrow {{E_{1M}}}  + \overrightarrow {{E_{2M}}} \)

Ta thấy \(\overrightarrow {{E_{1M}}}  \uparrow  \downarrow \overrightarrow {{E_{2M}}}  \Rightarrow E = {E_{1M}} - {E_{2M}}\)

Ta có: \({E_{1M}} = {E_{2M}} = k\frac{{\left| {{q_1}} \right|}}{{M{A^2}}} = {9.10^9}\frac{{\left| {{{16.10}^{ - 8}}} \right|}}{{{{\left( {{{5.10}^{ - 2}}} \right)}^2}}} \\= 5,{76.10^5}V/m\)

\( \Rightarrow E = {E_{1M}} - {E_{2M}} = 0\)

b)

NA = 5 cm, NB = 15 cm, AB = 10 cm nên N nằm ngoài AB và nằm trên đường thẳng AB.

Ta biểu diễn các vecto cường độ điện trường do hai điện tích gây ra tại điểm N như hình vẽ.

Vecto cường độ điện trường tại M là tổng hợp hai vecto \(\overrightarrow {{E_{1M}}} ,\overrightarrow {{E_{2M}}} \) 

Suy ra \(\overrightarrow E  = \overrightarrow {{E_{1M}}}  + \overrightarrow {{E_{2M}}} \)

Ta thấy: \(\overrightarrow {{E_{1M}}}  \uparrow  \uparrow \overrightarrow {{E_{2M}}}  \Rightarrow E = {E_{1M}} + {E_{2M}}\)

Ta có: \(\left\{ \begin{array}{l}{E_{1M}} = k\frac{{\left| {{q_1}} \right|}}{{A{N^2}}} = 5,{76.10^5}V/m\\{E_{2M}} = k\frac{{\left| {{q_2}} \right|}}{{B{N^2}}} = 0,{64.10^5}V/m\end{array} \right.\\ \Rightarrow E = 5,{12.10^5}V/m\)

Dạng 3: Xác định vị trí cường độ điện trường bằng 0

- Nếu \(\overrightarrow E  = \overrightarrow {{E_{1M}}}  + \overrightarrow {{E_{2M}}}  = \overrightarrow 0 \) thì \(\overrightarrow {{E_1}}  =  - \overrightarrow {{E_2}}  \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}}  \uparrow  \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right.\)

HocTot.Nam.Name.Vn