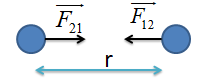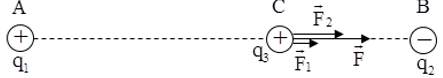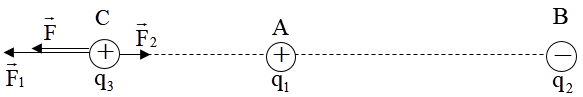Phương pháp giải một số dạng bài tập về điện tích – định luật Cu-lôngTổng hợp phương pháp giải một số dạng bài tập về điện tích - định Luật Cu-lông thường gặp Dạng 1: Xác định lực tương tác giữa hai điện tích và các đại lượng trong biểu thức định luật Cu-lông Áp dụng định luật Cu-lông. Lực tương tác giữa hai điện tích \({q_1},{q_2}\) đặt cách nhau một khoảng r trong môi trường có hằng số điện môi \(\varepsilon \) là \(\overrightarrow {{F_{12}}} ;\overrightarrow {{F_{21}}} \) có: - Điểm đặt: trên hai điện tích - Phương: nằm trên đường nối hai điện tích. - Chiều: + Hướng ra xa nhau nếu \({q_1}.{q_2} > 0\) (cùng dấu)
+ Hướng vào nhau nếu \({q_1}.{q_2} < 0\) (trái dấu)
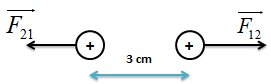
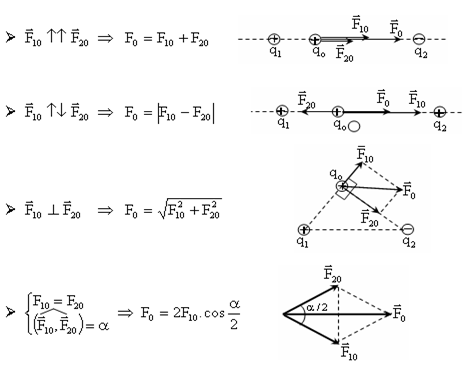
- Độ lớn: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\) với \(k = {9.10^9}\frac{{N.{m^2}}}{{{C^2}}}\) * Điều kiện áp dụng định luật: - Các điện tích là điện tích điểm - Các quả cầu đồng chất, tích điện đều, khi đó ta coi r là khoảng cách giữa hai tâm của quả cầu. Bài tập ví dụ: Cho hai điện tích \({q_1} = {6.10^{ - 8}}C\) và \({q_2} = {3.10^{ - 7}}C\) đặt cách nhau 3 cm trong chân không. a) Tính lực tương tác giữa chúng. b) Để lực này tăng lên 4 lần thì khoảng cách giữa chúng là bao nhiêu? c) Đưa hệ này vào nước có \(\varepsilon = 81\) thì lực tương tác giống câu a. Tìm khoảng cách giữa hai điện tích lúc này. Hướng dẫn giải a) Lực tương tác giữa hai điện tích được biểu diễn như hình vẽ: Và có độ lớn: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\frac{{\left| {{{6.10}^{ - 8}}{{.3.10}^{ - 7}}} \right|}}{{{{\left( {{{3.10}^{ - 2}}} \right)}^2}}} = 0,18N\) b) Khi lực tương tác giữa hai điện tích tăng lên 4 lần, ta có: \(F' = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon r{'^2}}} = 4F\) \( \Rightarrow \frac{F}{{F'}} = \frac{F}{{4F}} = \frac{{r{'^2}}}{{{r^2}}} \Leftrightarrow r{'^2} = \frac{{{3^2}}}{4} \Leftrightarrow r' = 1,5cm\) c) Đưa hệ này vào nước, lực tương tác không đổi: \(F = {9.10^9}\frac{{\left| {{{6.10}^{ - 8}}{{.3.10}^{ - 7}}} \right|}}{{81.r_3^2}} = 0,18N \Leftrightarrow r = 3,{3.10^{ - 3}}m\) Dạng 2: Tìm lực tổng hợp tác dụng lên một điện tích Áp dụng nguyên lý chồng chất điện trường: Khi một điện tích điểm q chịu tác dụng của nhiều lực tác dụng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,...,\overrightarrow {{F_n}} \) do các điện tích điểm \({q_1},{q_2},...,{q_n}\) gây ra thì hợp lực tác dụng lên q là: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} \) * Các bước tìm hợp lực \(\overrightarrow F \): Bước 1: Biểu diễn các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,...,\overrightarrow {{F_n}} \) bằng các vecto, gốc tại điểm ta xét. Bước 2: Vẽ vecto hợp lực theo quy tắc hình bình hành. Bước 3: Tính độ lớn của lực tổng hợp dựa vào phương pháp hình học hoặc định lý hàm cosin. * Các trường hợp đặc biệt: + \(\overrightarrow {{F_1}} \uparrow \uparrow \overrightarrow {{F_2}} \Rightarrow F = {F_1} + {F_2}\) + \(\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_2}} \Rightarrow F = \left| {{F_1} - {F_2}} \right|\) + \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_2}} \Rightarrow F = \sqrt {{F_1}^2 + {F_2}^2} \) + \(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right) = \alpha \Rightarrow F = \sqrt {{F_1}^2 + {F_2}^2 + 2{F_1}{F_2}\cos \alpha } \)
Bài tập ví dụ: Hai điện tích \({q_1} = {8.10^{ - 8}}C,{q_2} = - {8.10^{ - 8}}C\) đặt tại A,B trong không khí (AB = 6 cm). Xác định lực tác dụng lên \({q_3} = {8.10^{ - 8}}C\), nếu: a) CA = 4 cm, CB = 2 cm b) CA = 4 cm, CB = 10 cm Hướng dẫn giải Điện tích q3 sẽ chịu hai lực tác dụng của q1 và q2 là \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \). Lực tổng hợp : \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) a) Ta có: CA = 4 cm và CB = 2 cm => AC+CB = AB => C nằm trong đoạn AB Ta biểu diễn các lực tương tác như hình vẽ: Suy ra: \(\overrightarrow F \) cùng chiều với \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hướng từ C đến B) Độ lớn: \(F = {F_1} + {F_2} = k\frac{{\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} + k\frac{{\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = 0,18N\) b) CA = 4 cm và CB = 10 cm => CB – CA =AB => C nằm trên đường AB, ngoài khoảng AB về phía A. Ta biểu diễn các lực tương tác như hình vẽ: Ta thấy \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) ngược chiều nhau, \(\overrightarrow F \)cùng chiều với \(\overrightarrow {{F_1}} \) Độ lớn: Ta có: \({F_1} = k\frac{{\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = {9.10^9}\frac{{\left| {{{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = {36.10^{ - 3}}N\) \({F_2} = k\frac{{\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = {9.10^9}\frac{{\left| { - {{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{{{\left( {{{10.10}^{ - 2}}} \right)}^2}}} = 5,{76.10^{ - 3}}N\) \(F = \left| {{F_1} - {F_2}} \right| = 30,{24.10^{ - 3}}N\) Dạng 3. Con lắc tích điện 1. Cấu tạo con lắc tích điện Gồm: + Dây treo con lắc l + Vật tích điện có khối lượng m 2. Lực tác dụng khi vật mang điện có khối lượng Khi vật mang điện có khối lượng thì ngoài tác chịu tác dụng của lực điện do điện tích khác gây ra còn chịu thêm lực căng dây, trọng lực, lực đẩy acsimét. 3. Phương pháp - Bước 1: Tìm các lực và biểu diễn các lực tác dụng lên điện tích cần khảo sát - Bước 2: Hợp tất cả các lực tác dụng lên điện tích cần khảo sát, ta được: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} + \overrightarrow T = 0{\rm{ hay }}\overrightarrow {{F_i}} + \overrightarrow T = 0\) (Nếu con lắc tích điện ở vị trí cân bằng) Trong đó, \(\overrightarrow {{F_i}} \)có thể là: + Trọng lực \(\overrightarrow {{F_i}} \) + Lực điện do điện tích khác gây ra + Lực đẩy acsimet \(\overrightarrow {{F_i}} \)có: Phương - thẳng đứng, chiều - hướng lên, độ lớn FA = ρgV Với ρ - khối lượng riêng của chất lỏng hay khí (kg/m3) g - gia tốc rơi tự do V - phần thể tích của phần tử vật chìm trong chất lỏng hay khí - Bước 3: Tìm ẩn số của bài toán bằng 2 cách: + Cách 1: Sử dụng phương pháp chiếu + Cách 2: Nếu quy tắc hình bình hành là các hình thoi, hình chữ nhật, hình vuông thì sử dụng các hệ thức lượng trong tam giác, sử dụng định lí hàm số cos, tam giác đồng dạng,... Dạng 4. Sự cân bằng điện tích có khối lượng điện tích được bỏ qua Đối với dạng bài toán này sẽ hỏi vị trí q0 nào đó cần đặt ở đâu để các điện tích khác tác dụng lên q0 là cân bằng 1. Trường hợp 1:Tương tác 2 điện tích Dựa vào điều kiện cân bằng của 2 lực F1 và F2 tác dụng lên q0 \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow 0 \to \overrightarrow {{F_1}} = - \overrightarrow {{F_2}} \) Ta có: + F1, F2 cùng giá nên điện tích q0 nằm trên đường thẳng nối giữa q1 với q2 + Dự đoán điện tích cần khảo sát nằm ở vị trí nào, phụ thuộc vào dấu của 2 điện tích đã cho q1, q2 2. Trường hợp 2: Điện tích cần khảo sát q0 cân bằng với n điện tích đã cho đặt tại n đỉnh của 1 đa giác đều - Bước 1: + Dùng quy tắc tổng hợp của n -1 điện tích của đa giác tác dụng lên đỉnh còn lại:\(\sum\limits_{i = 1}^{n - 1} {\overrightarrow {{F_i}} } = \overrightarrow F \) + Xác định phương, chiều của hợp lực F của n -1 lực - Bước 2: Dùng điều kiện cân bằng tập hợp của n - 1 lực đặt tại đỉnh còn lại với lực cần khảo sát là \(\overrightarrow {{F_0}} \) (F0 là lực tác dụng lên điện tích còn lại) \(\overrightarrow F + \overrightarrow {{F_0}} = \overrightarrow 0 \to \overrightarrow F = - \overrightarrow {{F_0}} \) + F, F0 cùng giá → Xác định được vị trí q0 nằm trên đường nối giá của 2 lực F và F0 + Dự đoán dấu của điện tích q0 dựa vào dấu của điện tích còn lại.
|