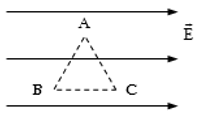
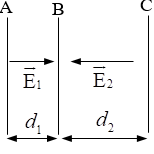
Phương pháp giải một số dạng bài tập về công của lực điện trường, điện thế, hiệu điện thế

Dạng 1: Tính công của các lực khi điện tích di chuyển

Sử dụng các công thức sau:

+ Công của lực điện trong điện trường đều: \(A = qEd\)

d > 0 khi hình chiếu cùng chiều đường sức

d < 0 khi hình chiếu ngược đường sức

+ \({A_{MN}} = {{\rm{W}}_{tM}} - {{\rm{W}}_{tN}} = {{\rm{W}}_{dM}} - {{\rm{W}}_{dN}}\)

+ \({A_{MN}} = {U_{MN}}.q = \left( {{V_M} - {V_N}} \right).q\)

Lưu ý: Dấu của công phụ thuộc vào dấu của q và U và góc hợp bởi chiều chuyển dời và chiều đường sức.

Bài tập ví dụ:

Điện tích \(q = {10^{ - 8}}C\) di chuyển dọc theo các cạnh của tam giác đều ABC cạnh a = 10 cm trong điện trường đều cường độ điện trường E = 300 V/m, \(\overrightarrow E //BC\). Tính công của lực điện trường khi q di chuyển trên mỗi cạnh của tam giác.

Hướng dẫn giải

Công của lực điện trường khi di chuyển trên các cạnh là:

\({A_{AB}} = qE.AB.\cos {120^0} = {10^{ - 8}}.300.0,1.\left( { - 0,5} \right)\\ =  - 1,{5.10^{ - 7}}J\)

\({A_{BC}} = qE.BC.\cos {0^0} = {10^{ - 8}}.300.0,1\\ = {3.10^{ - 7}}J\)

\({A_{CA}} = qE.AC.\cos {60^0} = {10^{ - 8}}.300.0,1.0,5\\ = 1,{5.10^{ - 7}}J\)

Dạng 2: Tìm điện thế - hiệu điện thế

Sử dụng các công thức sau:

- Điện thế: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)

Điện thế tại một điểm gây bởi điện tích q: \({V_M} = k\frac{q}{{\varepsilon r}}\)

Điện thế do nhiều điện tích gây ra: \(V = {V_1} + {V_2} + ... + {V_M}\)

Lưu ý: Người ta luôn chọn mốc điện thế tại mặt đất và ở vô cùng (bằng 0)

- Hiệu điện thế: \({U_{MN}} = \frac{{{A_{MN}}}}{q} = {V_M} - {V_N}\)

- Công thức liên hệ giữa cường độ điện trường và hiệu điện thế trong điện trường đều: \(E = \frac{U}{d}\)

Lưu ý: Trong điện trường, vecto cường độ điện trường có hướng từ nơi có điện thế cao sang nơi có điện thế thấp.

Bài tập ví dụ:

Cho ba bản kim loại phẳng A,B,C đặt song song như hình vẽ, cho d₁ = 5 cm và d₂ = 8 cm. Các bản được tích điện và điện tường giữa các bản là đều, có chiều như hình vẽ với độ lớn: \({E_1} = {4.10^4}V/m,{E_2} = {5.10^4}V/m\). Chọn gốc điện thế tại bản A, tìm điện thế \({V_B},{V_C}\) của hai bản B,C.

Hướng dẫn giải

Từ hình vẽ ta thấy \(\overrightarrow {{E_1}} \) hướng từ A đến B nên ta có: \({U_{AB}} = {V_A} - {V_B} = {E_1}.{d_1}\)

Chọn gốc điện thế tại A => \({V_A} = 0\)

\( \Rightarrow {V_B} = {V_A} - {E_1}{d_1} = 0 - {4.10^4}{.5.10^{ - 2}} =  - 2000V\)

\(\overrightarrow {{E_2}} \) hướng từ C đến B nên ta có:

\({U_{CB}} = {V_C} - {V_B} = {E_2}{d_2} \\\Leftrightarrow {V_C} = {V_B} + {E_2}{d_2} \\=  - 2000 + {5.10^4}{.8.10^{ - 2}} = 2000V\)

Dạng 3: Chuyển động của điện tích trong điện trường đều

Khi hạt mang điện bay vào trong điện trường với vận tốc ban đầu \(\overrightarrow {{v_0}} \) vuông góc với các đường sức điện. Hạt chịu tác dụng của lực điện không đổi có hướng vuông góc với \(\overrightarrow {{v_0}} \). Qũy đạo của hạt là một phần của đường parabol.

1. Gia tốc của điện tích:

Độ lớn gia tốc: \(a = \dfrac{F}{m} = \dfrac{{\left| q \right|E}}{m} = \dfrac{{\left| q \right|U}}{{m.d}}\)

Trong đó:

m: khối lượng của điện tích (kg); q: điện tích (C); U: hiệu điện thế (V)

d: khoảng cách giữa hai điểm dọc theo đường sức (m)

E: cường độ điện trường (V/m)

2. Chuyển động của điện tích dọc theo đường sức điện trường.

Chuyển động của điện tích dọc theo điện trường đều là chuyển động thẳng nhanh dần đều.

Áp dụng các công thức của chuyển động thẳng biến đổi đều:

\(v = {v_0} + at;s = {v_0}t + \frac{1}{2}a{t^2};{v^2} - v_0^2 = 2{\rm{a}}s\)

3. Chuyển động của điện tích vuông góc với đường sức điện trường.

Chuyển động của điện tích được coi như chuyển động ném ngang với vận tốc ban đầu v₀

Phương trình chuyển động: \(\left\{ \begin{array}{l}x = {v_0}t\\y = \frac{1}{2}a{t^2}\end{array} \right.\)=> phương trình quỹ đạo \(y = \frac{{a{x^2}}}{{2v_0^2}}\)

4. Chuyển động của điện tích hợp với đường sức góc \(\alpha \)

Chuyển động của điện tích được coi như chuyển động ném xiên với vận tốc v₀ hợp với phương ngang góc \(\alpha \)

Ta có: \(\left\{ \begin{array}{l}{v_x} = {v_0}\cos \alpha ;{v_y} = {v_0}\sin \alpha \\x = ({v_0}\cos \alpha )t;y = ({v_0}\sin \alpha )t + \frac{1}{2}a{t^2}\end{array} \right.\)

=>Phương trình quỹ đạo: \(y = \dfrac{{a{x^2}}}{{2{{({v_0}\cos \alpha )}^2}}} + x\tan \alpha \)