Phương pháp giải một số dạng bài tập về con lắc đơnTổng hợp cách giải một số dạng bài tập về con lắc đơn thường gặp Dạng 1: Chu kì con lắc đơn thay đổi theo chiều dài Chu kì con lắc đơn ban đầu khi chưa có sự thay đổi là: \({T_1} = \frac{1}{f} = 2\pi \sqrt {\frac{{{l_1}}}{g}} = \frac{{\Delta t}}{{{N_1}}}\) Chu kì của con lắc đơn sau khi có sự thay đổi là: \({T_2} = \frac{1}{f} = 2\pi \sqrt {\frac{{{l_2}}}{g}} = \frac{{\Delta t}}{{{N_2}}}\) => \(\frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{l_1}}}{{{l_2}}}} = \frac{{{N_2}}}{{{N_1}}}\) Trong đó N là số dao động toàn phần vật thực hiện được trong thời gian \(\Delta t\) *Bài toán con lắc vướng đinh: + Chu kì con lắc trước khi vướng đinh là: \({T_1} = 2\pi \sqrt {\frac{{{l_1}}}{g}} \) + Chu kì của con lắc sau khi vướng đinh là: \({T_2} = 2\pi \sqrt {\frac{{{l_2}}}{g}} \) => Chu kì của con lắc là: \(T = \frac{1}{2}\left( {{T_1} + {T_2}} \right)\) Bài tập ví dụ: Một con lắc đơn có chiều dài l. Trong khoảng thời gian \(\Delta t\) nó thực hiện 12 dao động. Khi giảm độ dài của nó bớt 16 cm, trong cùng khoảng thời gian \(\Delta t\) như trên, con lắc thực hiện 20 dao động. Tính độ dài ban đầu của con lắc. Hướng dẫn giải Ta có: \(\frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{l_1}}}{{{l_2}}}} = \frac{{{N_2}}}{{{N_1}}} \Leftrightarrow \sqrt {\frac{l}{{l - 0,16}}} = \frac{{20}}{{12}} \Leftrightarrow l = 0,25m\) Dạng 2: Xác định các đại lượng cơ bản trong dao động điều hòa của con lắc đơn - Tìm \(\omega ,{\rm{ }}{\bf{T}},{\rm{ }}{\bf{f}}\) : Đề cho l, g: \(\omega = \sqrt {\dfrac{g}{l}} ,T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{l}{g}} ,f = \dfrac{\omega }{{2\pi }} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{g}{l}} \) - Tìm gia tốc rơi tự do: \(T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{l}{g}} \to g = \dfrac{{4{\pi ^2}l}}{{{T^2}}}\) Dạng 3: Tìm \(\omega ,{\rm{ }}{\bf{T}},{\rm{ }}{\bf{f}}\) : thay đổi chiều dài dây treo l
Dạng 4: Viết phương trình dao động điều hòa của con lắc đơn
Sử dụng các dữ kiện đầu bài cho và hệ thức độc lập với thời gian: \(s_0^2 = {s^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)hay \(\alpha _0^2 = {\alpha ^2} + \dfrac{{{v^2}}}{{{l^2}{\omega ^2}}}\) hoặc \(\alpha _0^2 = {\alpha ^2} + \dfrac{{{v^2}}}{{lg}}\)
Tại \(t{\rm{ }} = {\rm{ }}0:\left\{ \begin{array}{l}s = {s_0}{\rm{cos}}\varphi \\v = - \omega {s_0}\sin \varphi \end{array} \right.\)
Với \({s_0} = l{\alpha _0}\) Bài tập ví dụ: Một con lắc đơn có chiều dài l = 16 cm. Kéo con lắc lệch khỏi vị trí cân bằng một góc 90 rồi thả nhẹ. Bỏ qua mọi ma sát, lấy g = 10 m/s2. Chọn gốc thời gian là lúc thả vật, chiều dương cùng chiều với chiều chuyển động ban đầu của vật. Viết phương trình dao động theo li độ góc tính ra rad. Hướng dẫn giải Ta có: phương trình dao động theo li độ góc của con lắc đơn có dạng: \(\alpha = {\alpha _0}\cos \left( {\omega t + \varphi } \right)\) Kéo con lắc lệch khỏi VTCB một góc 90 rồi thả nhẹ => \({\alpha _0} = {9^0} = \frac{\pi }{{20}} = 0,157ra{\rm{d}}\) \(\omega = \sqrt {\frac{g}{l}} = 2,5\pi ra{\rm{d}}/s\) Tại thời điểm t = 0 ta có: \(\alpha = {\alpha _0}\cos \varphi \Rightarrow \cos \varphi = \frac{\alpha }{{{\alpha _0}}} = \frac{{ - {\alpha _0}}}{{{\alpha _0}}} = - 1 \Rightarrow \varphi = \pi \) Vậy \(\alpha = 0,157\cos \left( {2,5\pi + \pi } \right)\left( {ra{\rm{d}}} \right)\) Dạng 5. Tính vận tốc vật ở li góc \(\alpha \) bất kì Phương pháp \({v_\alpha } = \pm \sqrt {2gl(c{\rm{os}}\alpha {\rm{ - cos}}{\alpha _0})} \) Đặc biệt:
Khi \({\alpha _0} \le {10^0}\) thì \({v_{{\rm{max}}}} = {\alpha _0}\sqrt {gl} = \omega {S_0}\) Dạng 6. Tính lực căng dây ở li độ góc \(\alpha \) bất kì Phương pháp \(T = mg(3c{\rm{os}}\alpha {\rm{ - 2cos}}{\alpha _0})\)
\(\begin{array}{l}T = mg(1 - 1,5{\alpha ^2}{\rm{ + }}{\alpha _0}^2)\\ \to {{\rm{T}}_{{\rm{max}}}} = mg(1{\rm{ + }}{\alpha _0}^2),{\rm{ }}{{\rm{T}}_{{\rm{min}}}} = mg(1 - 0,5{\alpha _0}^2)\end{array}\) Dạng 7: Năng lượng dao động, vận tốc, lực căng dây của con lắc đơn - Thế năng: \[{{\rm{W}}_t} = mgh = mgl(1 - \cos \alpha )\] - Động năng: \[{{\rm{W}}_d} = \frac{1}{2}m{v^2} = mgl\left( {\cos \alpha - \cos {\alpha _0}} \right)\] - Cơ năng: \[{\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = mgl\left( {1 - \cos {\alpha _0}} \right)\] - Vận tốc: \(\left\{ \begin{array}{l}v = \sqrt {2gl.\left( {\cos \alpha - \cos {\alpha _0}} \right)} \\{v_{\max }} = \sqrt {2gl.\left( {1 - \cos {\alpha _0}} \right)} \end{array} \right.\) - Lực căng dây: \(T = mg\left( {3\cos \alpha - 2\cos {\alpha _0}} \right)\) + \({T_{\max }} = mg\left( {3 - 2\cos {\alpha _0}} \right)\) (khi vật qua vị tri cân bằng) + \({T_{\min }} = mg.\cos {\alpha _0}\) (khi vật ở vị trí biên) *Lưu ý: Nếu \({\alpha _0} \le {10^0}\) thì \(\left\{ \begin{array}{l}{{\rm{W}}_t} = \frac{1}{2}mgl{\alpha ^2}\\{{\rm{W}}_d} = \frac{1}{2}mgl\left( {\alpha _0^2 - {\alpha ^2}} \right)\end{array} \right. \Rightarrow {\rm{W}} = \frac{1}{2}mgl\alpha _0^2\) (Với \(\alpha ,{\alpha _0}\) tính ra rad). Dạng 8. Sự thay đổi chu kì của con lắc đơn khi chịu thêm tác dụng của lực lạ 1. Các lực lạ thường gặp - Lực quán tính: \(\overrightarrow F = - m\overrightarrow a \), độ lớn F = ma ( \(\overrightarrow F \uparrow \downarrow \overrightarrow a \))  + Chuyển động nhanh dần đều \(\overrightarrow a \uparrow \uparrow \overrightarrow v \) (\(\overrightarrow v \) có hướng chuyển động) + Chuyển động chậm dần đều \(\overrightarrow a \uparrow \downarrow \overrightarrow v \) - Lực điện trường: \(\overrightarrow F = q\overrightarrow E \), độ lớn F = |q|E (Nếu q > 0 Þ \(\overrightarrow F \uparrow \uparrow \overrightarrow E \); còn nếu q < 0 Þ \(\overrightarrow F \uparrow \downarrow \overrightarrow E \)) - Lực đẩy Ácsimét: \(F = DgV\) (\(\overrightarrow F \)luông thẳng đứng hướng lên) Trong đó:
2. Công thức áp dụng làm bài tập - \(\overrightarrow F \) có phương ngang: \(\overrightarrow F \bot \overrightarrow P \) Tại VTCB dây treo lệch với phương thẳng đứng một góc có: \(\tan \alpha = \frac{F}{P}\) Thì \(g' = \sqrt {{g^2} + {{(\frac{F}{m})}^2}} \) Ví dụ: 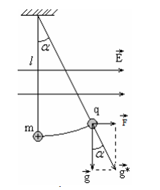 - \(\overrightarrow F \)có phương thẳng đứng thì \(g' = g \pm \frac{F}{m}\)
- \(\overrightarrow F \)có hướng xiên: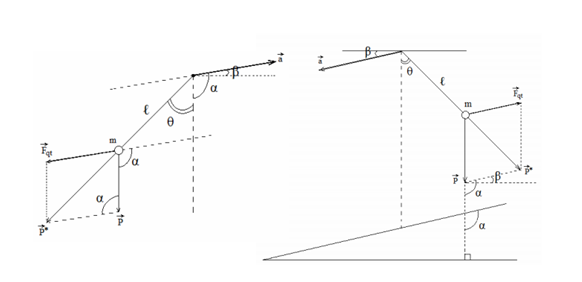 
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P.{F_{qt}}{\rm{cos}}\left( {{{90}^0} + \beta } \right)} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.ac{\rm{os(9}}{{\rm{0}}^0} + \beta )} \end{array}\) Góc θ: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} + \beta )}}\)
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P.{F_{qt}}{\rm{cos}}\left( {{{90}^0} - \beta } \right)} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.ac{\rm{os(9}}{{\rm{0}}^0} - \beta )} \end{array}\) Vì \(cos(\pi - a) = - cosa\) \( \to P' = \sqrt {{P^2} + F_{qt}^2 + 2P.{F_{qt}}{\rm{cos}}\alpha } \) Góc θ: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} - \beta )}}\) Dạng 9. Bài tập sự nhanh chậm của đồng hồ quả lắc1. Phương pháp chung Gọi T1 là chu kì chạy đúng, T2 là chu kì chạy sai Trong thời gian T1(s) đồng hồ chạy sai |T2-T1| (s) => 1(s) đồng hồ chạy sai \(\frac{{\left| {{T_2} - {T_1}} \right|}}{{{T_1}}}s\) Vậy trong khoảng thời gian ∆t, đồng hồ chạy sai: \(\theta = \Delta t\frac{{\left| {{T_2} - {T_1}} \right|}}{{{T_1}}}s\) Các bước giải: - Bước 1: Thiết lập tỉ số \(\frac{{{T_2}}}{{{T_1}}}\) - Bước 2: Biện luận:
- Bước 3: Xác định thời gian chạy nhau hay chậm bằng công thức: \(\theta = \Delta t\frac{{\left| {{T_2} - {T_1}} \right|}}{{{T_1}}} = \Delta t\left| {\frac{{{T_2}}}{{{T_1}}} - 1} \right|s\) 2. Các dạng bài tập a) Xác định thời gian đồng hồ chạy sai khi thay đổi nhiệt độ. - Khi thay đổi nhiệt độ, chiều dài của con lắc thay đổi theo biểu thức: \(l = {l_0}(1 + \alpha t)\)
Ở nhiệt độ t1 đồng hồ chạy đúng, nhiệt độ t2 đồng hồ chạy sai: - Xét tỉ số: \(\frac{{{T_2}}}{{{T_1}}}\) Ta có: \(\frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{{{l_2}}}{{{l_1}}}} = \sqrt {\frac{{{l_0}(1 + \alpha ({t_2})}}{{{l_0}(1 + \alpha {t_1})}}} = \sqrt {\frac{{(1 + \alpha {t_2})}}{{(1 + \alpha {t_1})}}} = {(1 + \alpha {t_2})^{\frac{1}{2}}}{(1 + \alpha {t_1})^{ - \frac{1}{2}}}\) Sử dụng công thức gần đúng: \(\left\{ \begin{array}{l}{\left( {1 \pm x} \right)^n} \approx 1 \pm nx\\\left( {1 + {x_1}} \right)\left( {1 - {x_2}} \right) \approx 1 + {x_1} - {x_2}\end{array} \right.\) với x, x1, x2 << 1 Vì αt1 và αt2<< 1\( \to {(1 + \alpha {t_2})^{\frac{1}{2}}}{(1 + \alpha {t_1})^{ - \frac{1}{2}}} \approx \left( {1 + \frac{1}{2}\lambda {t_2}} \right)\left( {1 - \frac{1}{2}\lambda {t_1}} \right) \approx 1 + \frac{1}{2}\alpha {t_2} - \frac{1}{2}\alpha {t_1} \approx 1 + \frac{1}{2}\alpha \left( {{t_2} - {t_1}} \right)\) \( \to \theta = \Delta t\frac{{\left| {{T_2} - {T_1}} \right|}}{{{T_1}}} = \Delta t\left| {\frac{{{T_2}}}{{{T_1}}} - 1} \right| = \Delta t.\frac{1}{2}\alpha \left( {{t_2} - {t_1}} \right)(s)\) Nếu t2 > t1: đồng hồ chạy chậm lại và ngược lại t2 < t1: đồng hồ chạy nhanh lên. b) Xác định thời gian đồng hồ chạy sai ở độ cao h và độ sâu d so với mực nước biến (coi nhiệt độ không đổi) Khi đưa con lắc lên độ cao h hay xuống độ sâu d thì gia tốc rơi tự do g thay đổi.
\(\left\{ \begin{array}{l}\frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{g}{{{g_h}}}} \\{g_h} = g\frac{{{R^2}}}{{{{\left( {R + h} \right)}^2}}}\end{array} \right. \to \frac{{{T_2}}}{{{T_1}}} = \frac{{\left( {R + h} \right)}}{R} = 1 + \frac{h}{R}\) \( \to \theta = \Delta t\frac{{\left| {{T_2} - {T_1}} \right|}}{{{T_1}}} = \Delta t\left| {\frac{{{T_2}}}{{{T_1}}} - 1} \right| = \Delta t\frac{h}{R}(s)\) Ta thấy \(\frac{{{T_2}}}{{{T_1}}} = 1 + \frac{h}{R} > 1 \to {T_2} > {T_1}\)=> Đồng hồ chạy chậm lại
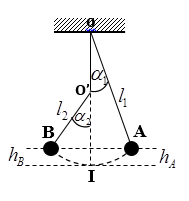
\(\left\{ \begin{array}{l}\frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{g}{{{g_d}}}} \\{g_d} = g\frac{{\left( {R - d} \right)}}{R}\end{array} \right. \to \frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{R}{{\left( {R - d} \right)}}} = \sqrt {\frac{1}{{1 - \frac{d}{R}}}} = {\left( {1 - \frac{d}{R}} \right)^{ - \frac{1}{2}}} \approx 1 + \frac{1}{2}\frac{d}{R}\) \( \to \theta = \Delta t\frac{{\left| {{T_2} - {T_1}} \right|}}{{{T_1}}} = \Delta t\left| {\frac{{{T_2}}}{{{T_1}}} - 1} \right| = \Delta t\frac{1}{2}\frac{d}{R}(s)\) Khi đưa con lắc lên cao hoặc xuống sâu, chu kì đều tăng nên suy ra đồng hồ luôn chạy chậm c) Xác định thời gian đồng hồ chạy sai khi thay đổi vị trí trên trái đất (nhiệt độ không đổi) Tại nơi có gia tốc trọng trường g1 đồng hồ chạy đúng với: \({T_1} = 2\pi \sqrt {\frac{l}{{{g_1}}}} \) Tại nơi có gia tốc trọng trường g2 đồng hồ chạy sai: \({T_1} = 2\pi \sqrt {\frac{l}{{{g_2}}}} \) \( \to \frac{{{T_2}}}{{{T_1}}} \approx 1 - \frac{1}{2}\frac{{\Delta g}}{{{g_1}}} \to \frac{{{T_2} - {T_1}}}{{{T_1}}} = - \frac{1}{2}\frac{{\Delta g}}{{{g_1}}}\) TỔNG QUÁT: Xác định thời gian đồng hồ chạy sai khi 1 hoặc nhiều yếu tố thay đổi. \(\frac{{\Delta T}}{T} = \frac{{{T_2} - {T_1}}}{{{T_1}}} = \frac{1}{2}\alpha \left( {{t_2} - {t_1}} \right) + \frac{h}{R} + \frac{1}{2}\frac{d}{R} - \frac{1}{2}\frac{{\Delta g}}{{{g_1}}}\) Dạng 10: Bài toán con lắc vướng đinh
Phương pháp: Một con lắc đơn đang dao động điều hòa với chiều dài ℓ1 thì con lắc vướng đinh làm cho nó dao động với ℓ2 nên chu kì, tần số góc, biên độ góc,… cũng thay đổi theo. Chu kì T của CLVĐ: \(T = \dfrac{1}{2}\left( {{T_1} + {T_2}} \right) \to T = \dfrac{\pi }{{\sqrt g }}(\sqrt {{l_1}} + \sqrt {{l_2}} )\) Vì \({W_A} = {W_B} \Rightarrow {h_A} = {\rm{ }}{h_B}\) Tỉ số biên độ dao động 2 bên VTCB – Góc lớn (α0>100): Vì \(h_A = h_B\) →ℓ1 (1–cosα1) = ℓ2(1–cosα2) \( \to \dfrac{{{l_1}}}{{{l_2}}} = \dfrac{{1 - c{\rm{os}}{\alpha _2}}}{{1 - c{\rm{os}}{\alpha _1}}}\) $\left( {{\alpha _0} \le {\rm{ }}{{10}^0}) \to cos\alpha \approx 1-{\alpha ^2}/2} \right): \to \dfrac{{{l_1}}}{{{l_2}}} = {(\dfrac{{{\alpha _2}}}{{{\alpha _1}}})^2}$ Dạng 11: Sự trùng phùng của hai con lắc Xét 2 con lắc dao động trong 2 mặt phẳng song song, con lắc 1 có chu kì T1, con lắc hai có chu kì T2 (T1>T2). Tại thời gian t = 0 hai con lắc có cùng 1 trạng thái (VD: cùng qua VTCB theochiều + chẳng hạn), sau thời gian nào đó trạng thái của 2 con lắc lại giống như trạng thái lúc t = 0 (tức lại cùng qua VTCB theo chiều +) được gọi là sự trùng phùng. Phương pháp: Thời gian ∆t nhỏ nhất kể từ khi thời điểm t = 0 cho tới lúc 2 còn lắc trùng phùng lần thứ nhất gọi là chu kì trùng phùng.
\(\begin{array}{l}n({T_1} - {T_2}) = {T_2} \leftrightarrow n{T_1} = (n + 1){T_2} = \Delta t\\ \to \Delta \tau = \dfrac{{{T_1}{T_2}}}{{\left| {{T_1} - {T_2}} \right|}}\end{array}\) hoặc \(\Delta t = b{T_1} = a{T_2}\) , trong đó: \(\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{a}{b}\) (phân số tối giản) Thời gian trùng phùng lần đầu kể từ lúc t = 0 cũng chính là chu kì trùng phùng \(\Delta \tau \) Bài tập ví dụ: Hai con lắc dao động điều hòa với chu kì lần lượt là \({T_1} = 2{\rm{s}};{T_2} = 1,5{\rm{s}}\). Giả sửtại thời điểm t hai con lăc cùng qua vị trí cân bằng theo cùng chiều thì sau đó bao lâu cả hai con lắc cùng qua vị trí cân bằng theo cùng chiều như trên. Hướng dẫn giải Gọi thời gian của hai con lắc cùng qua vị trí cân bằng theo cùng chiều là \(\Delta t\) (còn gọi là khoảng thời gian giữa hai lần trùng phùng liên tiếp). Ta có: \(\Delta t = {N_1}{T_1} = {N_2}{T_2}\) Theo bài ra ta có: \(\frac{{{T_1}}}{{{T_2}}} = \frac{{{N_2}}}{{{N_1}}} = \frac{2}{{1,5}} = \frac{4}{3}\)= phân số tối giản =>\(\left\{ \begin{array}{l}{N_1} = 3n\\{N_2} = 4n\end{array} \right.\left( {n \in N*} \right)\) Thời gian trùng phùng lần đầu tiên ứng với n = 1. Lúc đó con lắc 1 thực hiện được 3 dao động thì con lắc 2 thực hiện được 4 dao động nên thời gian trùng phùng là: \(\Delta t = 3{T_1} = 3.2 = 6s\) đối với con lắc 1 hoặc có thể là \(\Delta t = 4{T_2} = 4.1,5 = 6s\) đối với con lắc thứ hai Dạng 9. Bài toán con lắc đơn vướng đinh  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
