Phương pháp giải bài tập của chuyển động electron quang điện trong điện trường đều và từ trường đều

PHƯƠNG PHÁP GIẢI BÀI TẬP CỦA CHUYỂN ĐỘNG ELECTRON QUANG ĐIỆN TRONG ĐIỆN TRƯỜNG ĐỀU VÀ TỪ TRƯỜNG ĐỀU

1. CHUYỂN ĐỘNG CỦA ELECTRON QUANG ĐIỆN TRONG ĐIỆN TRƯỜNG ĐỀU

Electron chuyển động trong điện trường đều \(\overrightarrow E \), khi đó electron chịu tác dụng của lực điện trường \(\overrightarrow F  = e\overrightarrow E \), thu được gia tốc \(\overrightarrow a  = \frac{{\overrightarrow F }}{m} = \frac{{e\overrightarrow E }}{m}\) 

- Vận tốc trùng với phương của \(\overrightarrow E \)

• \(\overrightarrow v \uparrow  \uparrow \overrightarrow E \): Ta có: \(\overrightarrow F  \uparrow  \downarrow \overrightarrow E  \to \overrightarrow F  \uparrow  \downarrow \overrightarrow v \)

=> electron chuyển động chậm dần đều với gia tốc: \(a = \frac{F}{m} = \frac{{eE}}{m}\)

• \(\overrightarrow v \uparrow  \downarrow \overrightarrow E \): Ta có: \(\overrightarrow F  \uparrow  \downarrow \overrightarrow E  \to \overrightarrow F  \uparrow  \uparrow \overrightarrow v \)

=> electron chuyển động nhanh dần đều với gia tốc: \(a = \frac{F}{m} = \frac{{eE}}{m}\)

- \(\widehat {\overrightarrow v ,\overrightarrow E } = \alpha \)

Ta phân tích chuyển động của electron thành 2 chuyển động:

• Theo phương \( \bot \overrightarrow E \) : Chuyển động đều với vận tốc \({v_ \bot } = {v_0}\sin \alpha \)
• Theo phương \(//\overrightarrow E \): Chuyển động biến đổi đều với vận tốc \({v_{//}} = {v_0}{\rm{cos}}\alpha \)và gia tốc \(a = \frac{F}{m} = \frac{{eE}}{m}\)

Tính bán kính cực đại mà các electron đập vào bản dương (R_max)  ↔ Bài toán xác định tầm xa của vật ném xiên với vận tốc v₀ và góc nghiêng \(\alpha \)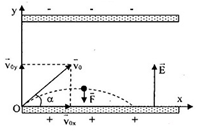

\({R_{{\rm{max}}}} = L = \frac{{v_0^2\sin 2\alpha }}{a}\)

2. CHUYỂN ĐỘNG CỦA ELECTRON QUANG ĐIỆN TRONG TỪ TRƯỜNG ĐỀU

Electron chuyển động trong từ trường đều \(\overrightarrow B \), khi đó electron chịu tác dụng của lực lorenxơ:  ${F_{L{\rm{orenxo}}}} = qvB\sin \alpha ;{\rm{ }}\left( {\alpha = \widehat {\overrightarrow v ,\overrightarrow B }} \right)$

- Khi vận tốc trùng với phương của \(\overrightarrow E \): electron chuyển động thẳng đều vì F_lorenxơ = 0.

- Khi \(\overrightarrow v \bot \overrightarrow B \): \( \to {F_{L{\rm{orenxo}}}} = qvB\) Lực F_L đóng vai trò là lực hướng tâm, electron chuyển động tròn đều với bán kính R

\(\frac{{{v^2}}}{R} = {a_{ht}} = \frac{F}{m} = \frac{{qvB}}{m} \to R = \frac{{mv}}{{qB}} = \frac{{mv}}{{eB}}\)