Trang chủ
Toán 9 cánh diều | Giải toán lớp 9 cánh diều

Lý thuyết Tần số. Tần số tương đối Toán 9 Cánh diều

1. Tần số và bảng tần số, biểu đồ tần số Tần số Một tập hợp gồm hữu hạn các dữ liệu thống kê được gọi là một mẫu. Số phần tử của một mẫu được gọi là kích thước mẫu (hay cỡ mẫu). Tần số của một giá trị là số lần xuất hiện giá trị đó trong mẫu dữ liệu.

1. Tần số và bảng tần số, biểu đồ tần số

Tần số

Một tập hợp gồm hữu hạn các dữ liệu thống kê được gọi là một mẫu. Số phần tử của một mẫu được gọi là kích thước mẫu (hay cỡ mẫu).

Tần số của một giá trị là số lần xuất hiện giá trị đó trong mẫu dữ liệu.

Lập bảng tần số

Để lập bảng tần số ở dạng bảng ngang, ta có thể làm như sau:

Bước 1. Xác định các giá trị khác nhau của mẫu dữ liệu và tìm tần số của mỗi giá trị đó.

Bước 2. Lập bảng gồm 2 dòng và một số cột

Theo thứ tự từ trên xuống dưới, ta lần lượt ghi:

- Cột đầu tiên: Tên các giá trị (x), Tần số (n)

- Các cột tiếp theo lần lượt ghi giá trị và tần số của giá trị đó

- Cột cuối cùng: Cộng, N = ...

Chú ý: Bảng tần số ở dạng bảng dọc được lập bằng cách tương tự như trên.

Ví dụ: Thống kê khối lượng rau thu hoạch một vụ (đơn vị: tạ) của mỗi hộ gia đình trong 38 hộ gia đình tham gia chương trình trồng rau theo tiêu chuẩn VIETGAP như sau:

Trong 38 số liệu thống kê ở trên có 7 giá trị khác nhau là:

\({x_1} = 4;{x_2} = 5;{x_3} = 6;{x_4} = 7;{x_5} = 8;{x_6} = 9;{x_7} = 10\)

Tần số của giá trị \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7}\) lần lượt là:

\({m_1} = 4;{m_2} = 7;{m_3} = 5;{m_4} = 8;{m_5} = 7;{m_6} = 5;{m_7} = 2\).

Bảng tần số của mẫu số liệu thống kê là:

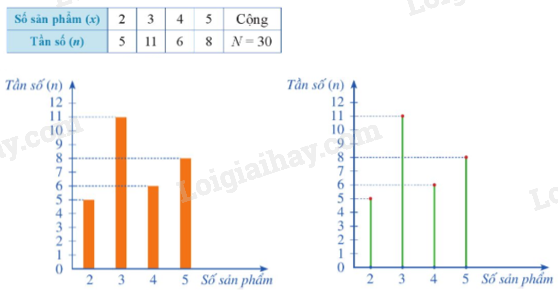
Vẽ biểu đồ tần số ở dạng biểu đồ cột hoặc biểu đồ đoạn thẳng

Bước 1. Lập bảng tần số của mẫu số liệu thống kê đó

Bước 2. Vẽ biểu đồ cột hoặc biểu đồ đoạn thẳng biểu diễn số liệu thống kê trong bảng tần số nhận được ở Bước 1.

Ví dụ: Biểu đồ tần số của mẫu số thống kê trong bảng tần số sau:

2. Tần số tương đối và bảng tần số tương đối, biểu đồ tần số tương đối ở dạng biểu đồ cột hoặc biểu đồ quạt tròn

Tần số tương đối

Tần số tương đối \({f_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số \({n_i}\) của của giá trị đó và số lượng N các dữ liệu trong mẫu dữ liệu thống kê: \({f_i} = \frac{{{n_i}}}{N}\).

Ta thường viết tần số tương đối dưới dạng phần trăm.

Lập bảng tần số tương đối ở dạng bảng ngang

Bước 1. Xác định các giá trị khác nhau của mẫu dữ liệu và tìm tần số tương đối của mỗi giá trị đó

Bước 2. Lập bảng gồm 2 dòng và một số cột

Theo thứ tự từ trên xuống dưới, ta lần lượt ghi:

- Cột đầu tiên: Tên các giá trị (x), Tần số tương đối (%)

- Các cột tiếp theo lần lượt ghi giá trị và tần số tương đối của giá trị đó

- Cột cuối cùng: Cộng, 100.

Chú ý: Bảng tần số tương đối ở dạng bảng dọc được lập bằng cách tương tự như trên.

Ví dụ: Cho bảng thống kê số anh, chị, em ruột của các bạn trong lớp:

Tổng số bạn là \(n = 30\).

Số anh, chị, em ruột là \({x_1} = 0;{x_2} = 1;{x_3} = 2;{x_4} = 3\) tương ứng với \({m_1} = 8;{m_2} = 12;{m_3} = 6,{m_4} = 4\).

Do đó các tần số tương đối cho các giá trị \({x_1},{x_2},{x_3},{x_4}\) lần lượt là:

\({f_1} = \frac{8}{{30}} \approx 26,7\% ;{f_2} = \frac{{12}}{{30}} = 40\% ;{f_3} = \frac{6}{{30}} = 20\% ;{f_4} = \frac{4}{{30}} \approx 13,3\% \).

Ta có bảng tần số tương đối sau:

Vẽ biểu đồ tần số ở dạng biểu đồ cột

Để vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột của một mẫu dữ liệu thống kê, ta có thể thực hiện các bước sau:

Bước 1. Lập bảng tần số tương đối của mẫu số liệu thống kê đó

Bước 2. Vẽ biểu đồ cột biểu diễn số liệu thống kê trong bảng tần số tương đối nhận được ở Bước 1.

Vẽ biểu đồ tần số ở dạng biểu đồ hình quạt tròn

Để vẽ biểu đồ tần số tương đối ở dạng biểu đồ hình quạt tròn của một mẫu dữ liệu thống kê, ta có thể thực hiện các bước sau:

Bước 1. Lập bảng tần số tương đối của mẫu dữ liệu thống kê đó

Bước 2. Vẽ biểu đồ hình quạt tròn biểu diễn số liệu thống kê trong bảng tần số tương đối nhận được ở Bước 1.

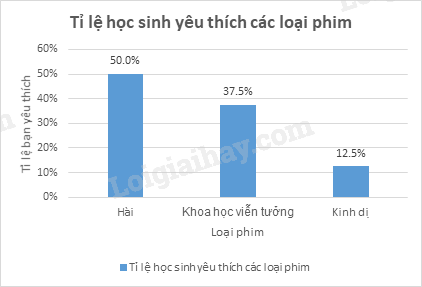
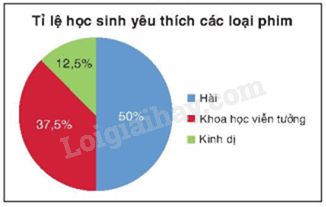
Ví dụ: Cho bảng tần số tương đối về loại phim yêu thích của các học sinh trong lớp 9A như sau:

Biểu đồ tần số tương đối ở dạng biểu đồ cột của mẫu số liệu thống kê đó là:

Biểu đồ tần số tương đối ở dạng biểu đồ hình quạt tròn của mẫu số liệu thống kê đó là:

  • Giải mục 1 trang 16, 17, 18 SGK Toán 9 tập 2 - Cánh diều

    Sau khi điều tra 60 hộ gia đình ở một vùng dân cư về số nhân khẩu của mỗi hộ gia đình, người ta được dãy số liệu thống kê (hay còn gọi là mẫu số liệu thống kê) như sau: a) Trong 60 số liệu thống kê ở trên, có bao nhiêu giá trị khác nhau? b) Mỗi giá trị đó xuất hiện bao nhiêu lần?

  • Giải mục 2 trang 19, 20, 21 SGK Toán 9 tập 2 - Cánh diều

    Xét mẫu số liệu thống kê ở Ví dụ 1 với bảng tần số là Bảng 20. Tính tỉ số phần trăm của tần số ({n_1} = 6)và số học sinh của lớp 9C.

  • Giải bài tập 1 trang 23 SGK Toán 9 tập 2 - Cánh diều

    Thống kê điểm sau 46 lần bắn bia của một xạ thủ như sau: a) Lập bảng tần số của mẫu số liệu thống kê đó. b) Vẽ biểu đồ tần số ở dạng biểu đồ đoạn thẳng và biểu đồ cột của mẫu số liệu thống kê đó.

  • Giải bài tập 2 trang 23 SGK Toán 9 tập 2 - Cánh diều

    Gieo một xúc xắc 32 lần liên tiếp, ghi lại số chấm trên mặt xuất hiện của xúc xắc, ta được mẫu số liệu thống kê như sau: a) Lập bảng tần số tương đối của mẫu số liệu thống kê đó. b) Vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột và biểu đồ hình quạt tròn của mẫu số liệu thống kê đó.

  • Giải bài tập 3 trang 23 SGK Toán 9 tập 2 - Cánh diều

    Kết quả đánh giá chất lượng bằng điểm của 40 sản phẩm được cho trong Bảng 25. a) Lập bảng tần số tương đối của mẫu số liệu thống kê đó. b) Vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột và biểu đồ hình quạt tròn của mẫu số liệu thống kê đó.

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
close

Tiện ích | Blog

Nội dung từ Loigiaihay.Com