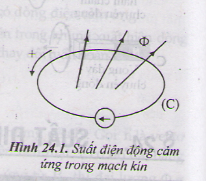
Lý thuyết suất điện động cảm ứngI . SUẤT ĐIỆN ĐỘNG CẢM ỨNG TRONG MẠCH KÍN SUẤT ĐIỆN ĐỘNG CẢM ỨNG I . SUẤT ĐIỆN ĐỘNG CẢM ỨNG TRONG MẠCH KÍN1.Định nghĩaSự xuất hiện dòng cảm ứng trong một mạch kín (C) chứng tỏ tồn tài một nguồn điện trong mạch đó. Suất điện động của nguồn này được gọi là suất điện động cảm ứng. Vậy có thể định nghĩa: Suất điện động cảm ứng là suất điện động sinh ra dòng điện cảm ứng trong mạch kín. 2. Định luât Fa – ra – đâyGiả sử mạch kín (C) đặt trong một từ trường, từ thông qua mạch biến thiên một đại lượng ∆Φ trong một khoảng thời gian ∆t. Giả sử sự biến thiên từ thông này được thực hiện qua một dịch chuyển nào đó của mạch. Trong dịch chuyển này, lực tương tác tác dụng lên mạch (C) đã sinh ra một công ∆A. Người ta đã chứng minh được rằng ∆A = i∆Φ Với I là cường độ dòng điện cảm ứng. Theo định luật len – xơ, lực từ tác dụng lên mạch (C) luôn cản trở chuyển động tạo ra biến thiên từ thông. Do đó ∆A là một công cản.Vậy, để thực hiện sự dịch chuyển của (C) (nhằm tạo ra sự biến thiên của Φ) phải có ngoại lực tác dụng lên (C) và trong chuyển dời nói trên, ngoại lực này sinh công thắng công cản của lực từ. ∆A’ = -∆A = -i∆Φ (24.1) Công ∆A’ có độ lớn bằng tổng phần năng lượng do bên ngoài cung cấp cho mạch (C) và được chuyển hóa thành điện năng của suất điện động cảm ứng ec (tương tự như điện năng do một nguồn điện sản ra) trong khoảng thời gian ∆t. Theo công thức (7.3) ta có: ∆A’ = eci∆t (24.2) So sánh hai công thức của ∆A’ ta suy ra công thức của suất điện động cảm ứng: |ec| = \(|\frac{\Delta \Phi }{\Delta t}|\) (24.3) Nếu chỉ xét độ lớn của ec (không kể dấu) thì : Thương số \(|\frac{\Delta \Phi }{\Delta t}|\) biểu thị độ biến thiên từ thông qua mạch (C) trong một đơn vị thời gian, thương số này được gọi là tốc độ biến thiên từ thông qua mạch. Vậy công thức (24.4) được phát biểu như sau : Độ lớn của suất điện động cảm ứng xuất hiện trong mạch kín tỉ lệ với tốc độ biến thiên từ thông qua mạch kín đó. Phát biểu này được gọi là định luật cơ bản của hiện tượng cảm ứng điện từ - định luật Fa –ra đây.
II. SUẤT ĐIỆN ĐỘNG CẢM ỨNG VÀ ĐỊNH LUẬT LEN – XƠSự xuất hiện dấu (-)trong công thức (24.3) là để phù hợp với định luật Len – xơ Trước hết mạch kín (C) phải được định hướng. Dựa vào chiều đã chọn trên (C) , ta chọn chiều pháp tuyến dương để tính từ thông Φ qua mạch kín (C) (Φ là một đại lượng đại số). Nếu Φ tăng thì ec < 0: chiều của suất điện động cảm ứng (chiều của dòng điện cảm ứng) ngược với chiều của mạch Nếu Φ giảm thì ec > 0: chiều của suất điện động cảm ứng (chiều của dòng điện cảm ứng) là chiều của mạch III. QUY TẮC BÀN TAY PHẢIĐặt bàn tay phải hứng các đường sức từ, ngón cái choãi ra 900 hướng theo chiều chuyển động của đoạn dây, khi đó đoạn dây dẫn đóng vai trò như một nguồn điện, chiều từ cổ tay đến bốn ngón tay chỉ chiều từ cực âm sang cực dương của nguồn điện đó 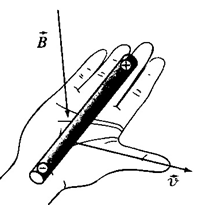
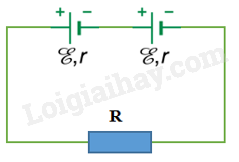
+ Khi mạch được nối kín thì trong mạch có dòng điện cảm ứng iC + Bên trong nguồn điện, dòng điện có chiều từ cực âm sang cực dương, bên ngoài thì ngược lại. IV. BIỂU THỨC SUẤT ĐIỆN ĐỘNG CẢM ỨNG TRONG ĐOẠN DÂY\(\left| {{e_C}} \right| = Blv\sin \theta \) Trong đó: + eC : suất điện động cảm ứng của đoạn dây (V) + B: cảm ứng từ (T) + \(l\) : chiều dài đoạn dây (m) + v: vận tốc của đoạn dây + \(\theta {\rm{ = }}\left( {\overrightarrow v ,\overrightarrow B } \right)\) Dây dẫn chuyển động trong từ trường được coi như một nguồn điện. Khi đó, lực lorenxơ tác dụng lên các electron đóng vai trò lực lạ tạo thành dòng điện V. CHUYỂN HÓA NĂNG LƯỢNG TRONG HIỆN TƯỢNG CẢM ỨNG ĐIỆN TỪTrong hiện tượng cảm ứng điện từ trên đây, để tạo ra sự biến thiên từ thông qua mạch (C), phải có ngoại lực tác dụng vào (C) và ngoại lực này sinh ra một công cơ học. Công cơ học này làm xuất hiện suất điện động cảm ứng trong mạch, nghĩa là đã tạo ra điện năng. Vậy bản chất của hiện tượng cảm ứng điện từ đã nêu trên là quá trình chuyển hóa cơ năng thành điện năng. Fa- ra – đây là người đầu tiên khám phá ra hiện tượng cảm ứng điện từ và định luật cơ bản về hiện tượng này. Đóng góp của Fa- ra – đây đã mở ra một triển vọng to lớn trong thế kỉ XIX về một phượng thức sản xuất điện năng mới, làm cơ sở cho công cuộc điện khí hóa. VI. MÁY PHÁT ĐIỆN- Là ứng dụng quan trọng và quen thuộc của hiện tượng cảm ứng điện từ trong các đoạn dây chuyển động + Máy phát điện xoay chiều: 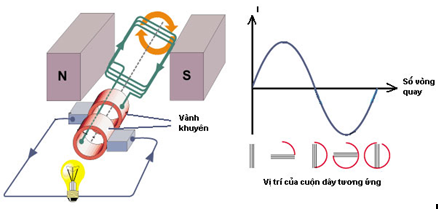 + Máy phát điện một chiều: 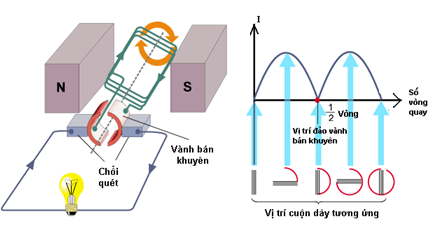 VII. BÀI TẬP VẬN DỤNGCâu 1: Hai nguồn điện giống nhau, mỗi nguồn có suất điện động 1,5V và điện trở trong 0,5 Ω được mắc với một điện trở 2Ω thành sơ đồ mạch điện như sau:
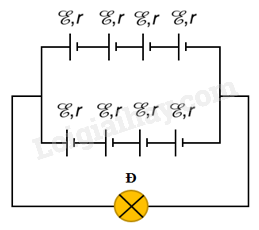
a) Tính suất điện động và điện trở trong của bộ nguồn b) Tính cường độ dòng điện trong mạch. Lời giải chi tiết a) Sơ đồ cho thấy hai nguồn mắc nối tiếp, suất điện động và điện trở trong của bộ nguồn là: ξb = 2ξ = 2.1,5 = 3 (V); rb = 2 r = 2.0,5 = 1(Ω) b) Áp dụng định luật Ôm cho toàn mạch \(I = \frac{{{\xi _b}}}{{R + {r_b}}} = \frac{3}{{2 + 1}} = 1A\) Câu 2: Có tám nguồn điện cùng loại với cùng suất điện động ξ = 1,5 V và điện trở trong r = 1 Ω. Mắc các nguồn này thành bộ hỗn hợp đối xứng gồm hai dãy song song để thắp sáng bóng đèn loại 6V - 6W. Coi như bóng đèn có điện trở như khi sáng bình thường. a) Vẽ sơ đồ mạch điện kín gồm bộ nguồn và bóng đèn ở mạch ngoài. b) Tính cường độ dòng điện I qua bóng đèn và công suất tiêu thụ của đèn khi đó. Lời giải chi tiết a) Sơ đồ mạch:
b) Suất điện động và điện trở trong của bộ nguồn \(\xi \)b = 4e = 6 (V) ; rb = \(\frac{{4r}}{2}\) = 2r = 2 (W) Điện trở của bóng đèn RĐ = \(\frac{{U_{dm}^2}}{{{P_{dm}}}}\) = 6 (W) = RN Cường độ dòng điện chạy qua đèn I = \(\frac{\xi }{{{R_N} + r}}\) = 0,75 (A) Công suất của bóng đèn khi đó PĐ = I2RĐ = 0,752.6 = 3,375 (W) Nhận xét: Khi đó đèn sáng yếu hơn bình thường. Sơ đồ tư duy về suất điện động cảm ứng
|