Lý thuyết Số thập phân Toán 6 Chân trời sáng tạoTải vềLý thuyết Số thập phân Toán 6 Chân trời sáng tạo ngắn gọn ,đầy đủ, dễ hiểu Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... I. Phân số thập phân và số thập phân âmPhân số thập phân là là phân số mà mẫu là lũy thừa của $10$. Ví dụ: $\dfrac{7}{{10}};\dfrac{{ - 15}}{{1000}};...$ là các phân số thập phân. - Ta viết $ - \dfrac{{15}}{{10}} = - 1,5$ và gọi $ - 1,5$ là số thập phân âm, đọc là “ âm một phẩy năm”. - Các số $2,3;\,\,0,24;...$gọi là các số thập phân dương, đôi khi còn được viết là $ + 2,3;\,\, + 0,24;...$ - Các số thập phân dương và các số thập phân âm gọi chung là số thập phân. Nhận xét: - Mọi phân số thập phân đều viết được dưới dạng số thập và ngược lại. - Số thập phân gồm hai phần: + Phần số nguyên viết bên trái dấu phẩy; + Phần thập phân viết bên phải dấu phẩy. II. So sánh hai số thập phân- Số thập phân âm nhỏ hơn $0$ và nhỏ hơn số thập phân dương - Nếu $a,b$ là hai số thập phân dương và $a > b$ thì $ - a < - b$. Ví dụ: a) $2,34 < 5,21$ b) Do $2,3 > 1,5$ nên $ - 2,3 < - 1,5$. Chú ý: Nếu $a < b$ và $b < c$ thì $a < c$. III. Số đối của một số thập phânHai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau. Ví dụ: Số đối của $ - 1,5$ là $1,5$. Số đối của 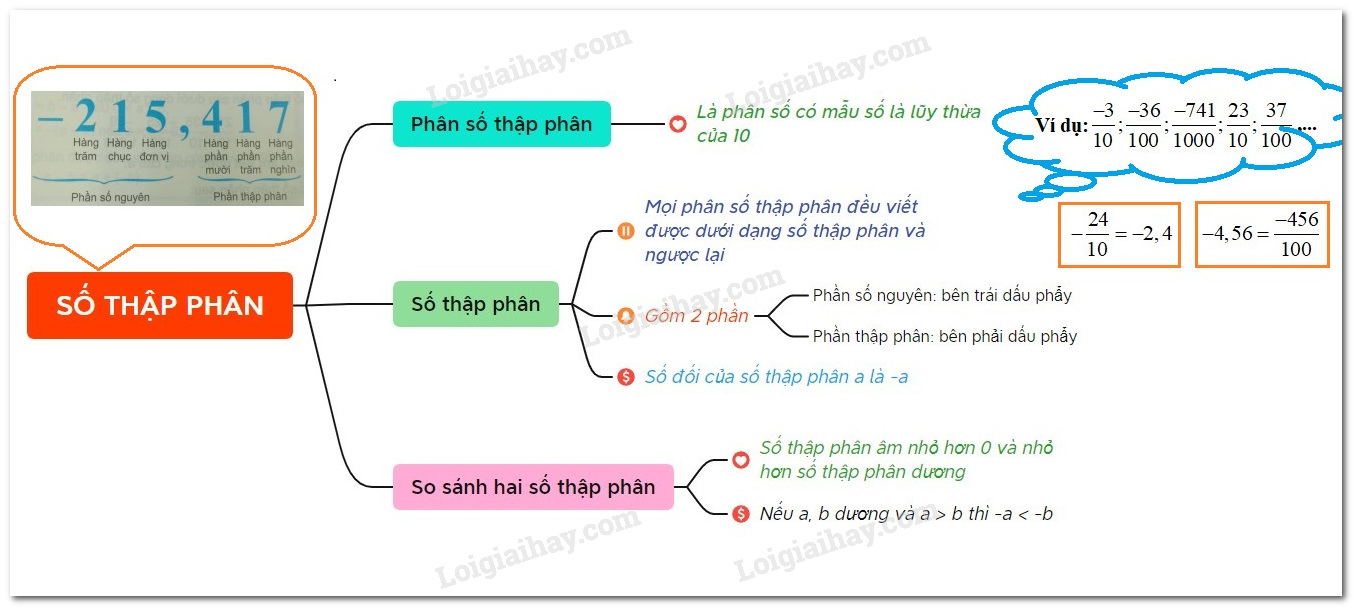$24,3$ là $ - 24,3$
 Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
