Lý thuyết So sánh phân số. Hỗn số dương Toán 6 Cánh diều

1. So sánh các phân số:

Trong 2 phân số khác nhau luôn có một phân số lớn hơn phân số kia

*Phân số lớn hơn 0 gọi là phân số dương

*Phân số nhỏ hơn 0 gọi là phân số âm

*Nếu phân số $\frac{a}{b}$ nhỏ hơn phân số $\frac{c}{d}$ thì ta viết $\frac{a}{b}< \frac{c}{d}$ hay $\frac{c}{d}> \frac{a}{b}$ 

*Nếu $\frac{a}{b}< \frac{c}{d}$ và $\frac{c}{d}< \frac{e}{g}$  thì $\frac{a}{b}< \frac{e}{g}$ 

a) So sánh hai phân số cùng mẫu

Ví dụ: So sánh $\dfrac{{ - 4}}{5}$ và $\dfrac{{ - 7}}{5}$.

Ta có: $- 4 > - 7$ và $5 > 0$ nên $\dfrac{{ - 4}}{5} > \dfrac{{ - 7}}{5}$.

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

Ví dụ:

So sánh $\dfrac{{ - 4}}{{ - 5}}$ và $\dfrac{2}{{ - 5}}$

Đưa hai phân số trên về có cùng một mẫu nguyên âm: $\dfrac{4}{5}$ và $\dfrac{{ - 2}}{5}$

Ta có: $4 > - 2$ và $5 > 0$ nên $\dfrac{4}{5} > \dfrac{{ - 2}}{5}$.

b) So sánh hai phân số khác mẫu

Ví dụ: So sánh hai phân số $\dfrac{{ - 7}}{{12}}$ và $\dfrac{{ - 11}}{{18}}$.

$BCNN(12;18) = 36$ nên ta có:

$\dfrac{{ - 7}}{{12}} = \dfrac{{ - 7.3}}{{12.3}} = \dfrac{{ - 21}}{{36}}$

$\dfrac{{ - 11}}{{18}} = \dfrac{{ - 11.2}}{{18.2}} = \dfrac{{ - 22}}{{36}}$.

Vì $- 21 > - 22$ nên $\dfrac{{ - 21}}{{36}} > \dfrac{{ - 22}}{{36}}$. Do đó $\dfrac{{ - 7}}{{12}} > \dfrac{{ - 11}}{{18}}$.

c) Áp dụng quy tắc so sánh phân số

Ví dụ: $\dfrac{{ - 3}}{{ - 5}} > 0$ hoặc $\dfrac{4}{5} > 0$

Ví dụ : $\dfrac{{ - 3}}{5} < 0$

- Ta còn có các cách so sánh phân số như sau:

+ Áp dụng tính chất: $\dfrac{a}{b} < \dfrac{c}{d} \Leftrightarrow a.d < b.c{\rm{\;}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in {\rm{Z}};{\rm{b}},{\rm{d\;}} > {\rm{\;0}})$

+ Đưa về hai phân số cùng tử dương rồi so sánh mẫu (chỉ áp dụng đối với hai phân số cùng âm hoặc cùng dương)

Ví dụ: $\dfrac{4}{{ - 9}} > \dfrac{4}{{ - 7}};$$\dfrac{3}{5} < \dfrac{3}{2}$

+ Chọn số thứ ba làm trung gian.

Ví dụ:

$\dfrac{{ - 4}}{9} < 0 < \dfrac{4}{7}{\kern 1pt}$ suy ra $\dfrac{{ - 4}}{9}<\dfrac{4}{7}$

$\dfrac{{14}}{9} > 1 > \dfrac{4}{7}$ suy ra $\dfrac{{14}}{9}>\dfrac{4}{7}$

+ Sử dụng tính chất so sánh: Nếu $\dfrac{a}{b} < 1$ thì $\dfrac{a}{b} < \dfrac{{a + m}}{{b + m}}$

2. Hỗn số dương

Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 ( với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.

Ví dụ: 

$\frac{7}{4}= \frac{4.1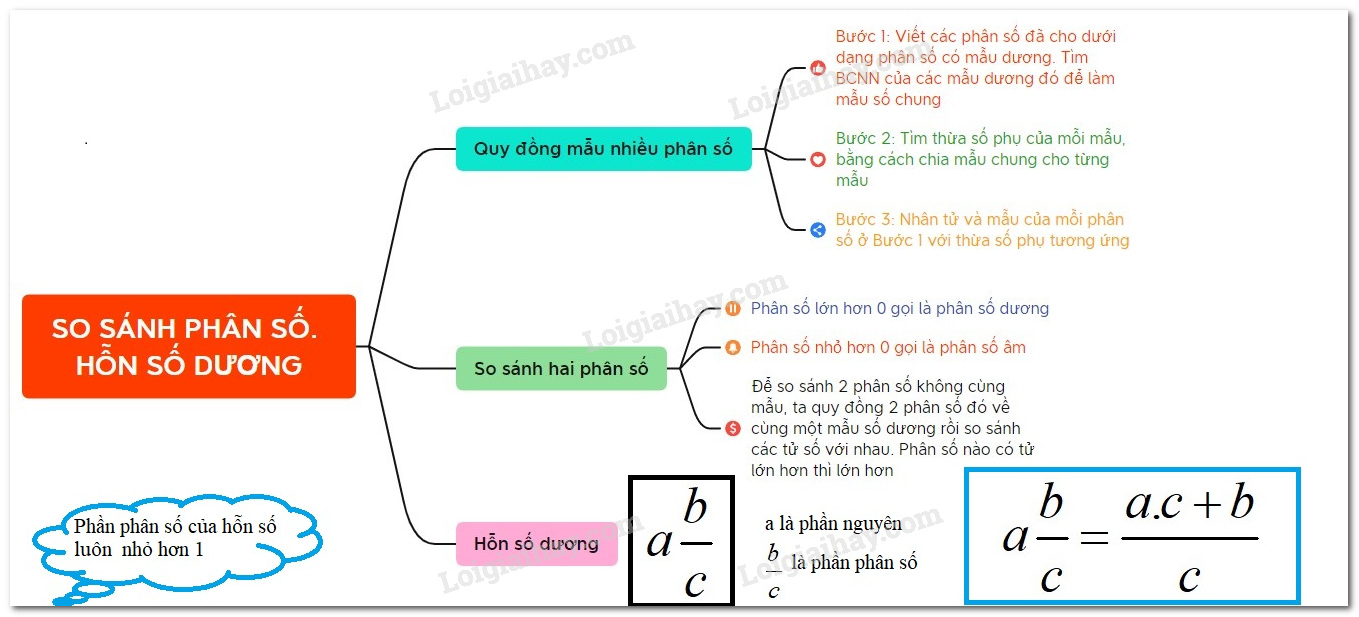+3}{4}= 1 + \frac{3}{4}=1\frac{3}{4}$