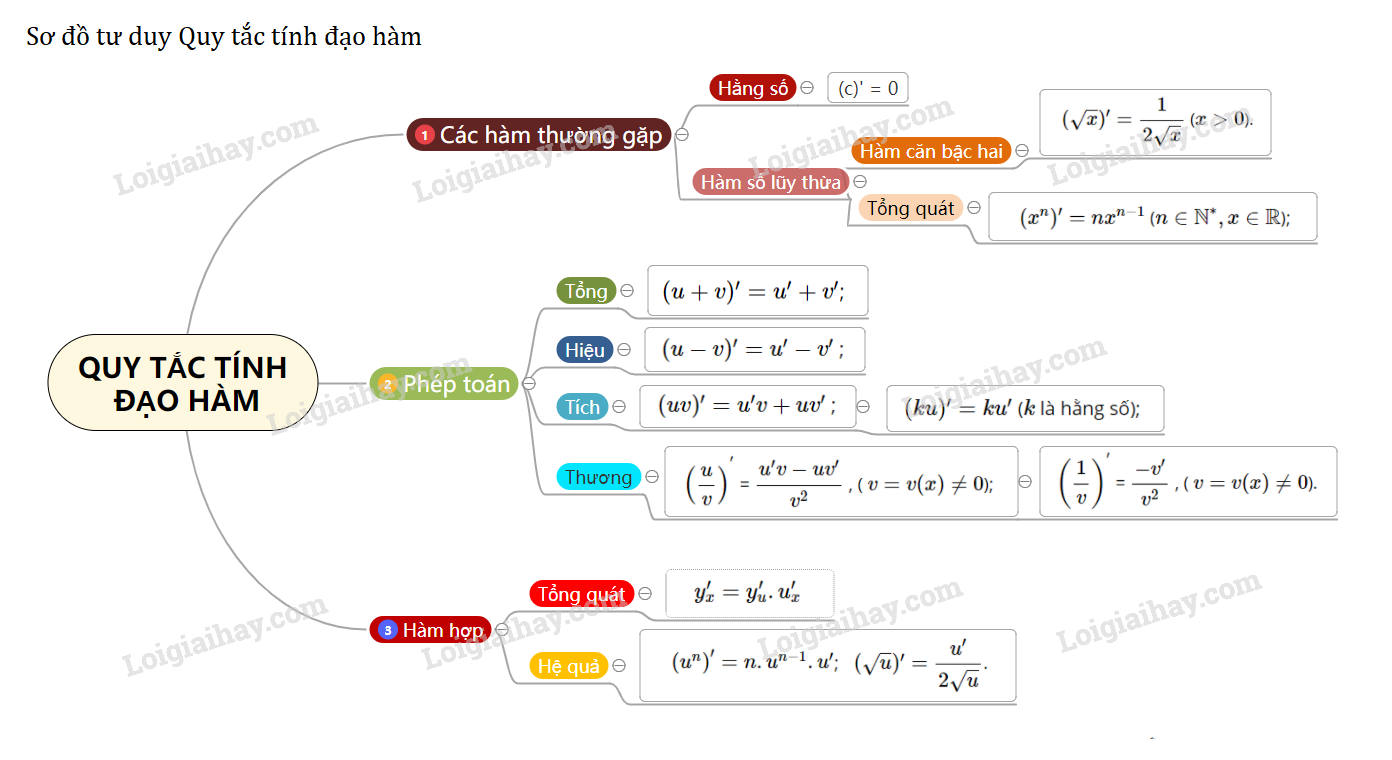
Lý thuyết Quy tắc tính đạo hàmTổng hợp lí thuyết về Quy tắc tính đạo hàm đầy đủ, ngắn gọn dễ hiểu 1. Công thức (c)′=0 ( c là hằng số); (xn)′=nxn−1 (n∈N∗,x∈R); (√x)′=12√x (x>0). 2. Phép toán (u+v)′=u′+v′; (u−v)′=u′−v′ ; (uv)′=u′v+uv′ ; (ku)′=ku′ (k là hằng số); (uv)′ = u′v−uv′v2 , ( v=v(x)≠0); (1v)′ = −v′v2 , ( v=v(x)≠0). 3. Đạo hàm của hàm hợp y′x=y′u.u′x Hệ quả: +) (un)′=n.un−1.u′; +) (√u)′=u′2√u.
 Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
