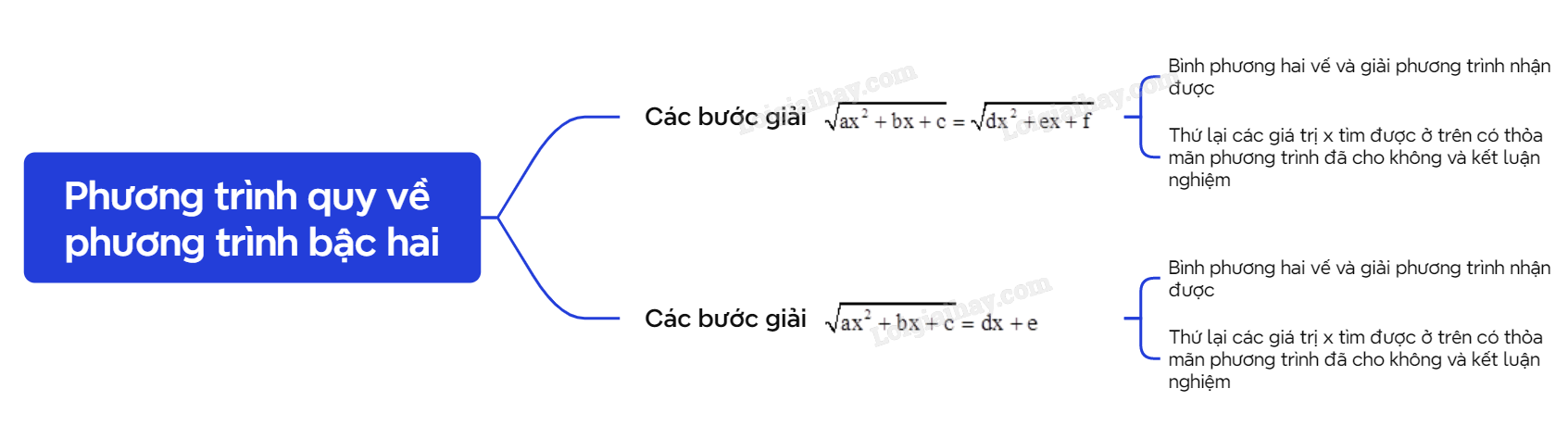
Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Kết nối tri thức

A. Lý thuyết 1. Phương trình dạng $\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f}$

Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

A. Lý thuyết

1. Phương trình dạng $\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f}$

Để giải phương trình $\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f}$ , ta thực hiện như sau:

- Bình phương hai vế và giải phương trình nhận được.

- Thứ lại các giá trị x tìm được ở trên có thỏa mãn phương trình đã cho không và kết luận nghiệm.

2. Phương trình dạng $\sqrt {a{x^2} + bx + c} = dx + e$

Để giải phương trình $\sqrt {a{x^2} + bx + c} = dx + e$ , ta thực hiện như sau:

- Bình phương hai vế và giải phương trình nhận được.

- Thứ lại các giá trị x tìm được ở trên có thỏa mãn phương trình đã cho không và kết luận nghiệm.

B. Bài tập

Bài 1: Giải phương trình $\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2}$ .

Giải:

Bình phương hai vế của phương trình, ta được $2{x^2} - 4 - 2 = {x^2} - x - 2$ .

Sau khi thu gọn, ta được ${x^2} - 3x = 0$ . Từ đó tìm được x = 0 hoặc x = 3.

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 3 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 3.

Bài 2: Giải phương trình $\sqrt {2{x^2} - 5x - 9} = x - 1$ .

Giải:

Bình phương hai vế của phương trình, ta được $2{x^2} - 5x - 9 = {x^2} - 2x + 1$ .

Sau khi thu gọn, ta được ${x^2} - 3x - 10 = 0$ . Từ đó tìm được x = -2 hoặc x = 5.

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 5 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 5.

Chia sẻ

Bình luận

Bình chọn:

3.8 trên 4 phiếu

Giải mục 1 trang 25 SGK Toán 10 tập 2 - Kết nối tri thức
a) Bình phương hai vế của phương trình để khử căn và giải phương trình bậc hai nhận được b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không Giải các phương trình sau:
Giải mục 2 trang 25, 26 SGK Toán 10 tập 2 - Kết nối tri thức
Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở Thôn Hoành,
Giải bài 6.20 trang 27 SGK Toán 10 – Kết nối tri thức
Giải các phương trình sau:
Giải bài 6.21 trang 27 SGK Toán 10 – Kết nối tri thức
Giải các phương trình sau:
Giải bài 6.22 trang 27 SGK Toán 10 – Kết nối tri thức
(H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD

Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.