Lý thuyết Ôn tập chương 2. Đường trònLý thuyết Ôn tập chương 2. Đường tròn 1. Sự xác định đường tròn, tính chất đối xứng của đường tròn. a) Đường tròn tâm \(O\) bán kính \(R\left( {R > 0} \right)\) là hình gồm các điểm cách điểm \(O\) một khoảng bằng \(R\). b) Vị trí tương đối của một điểm đối với một đường tròn. Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\). +) \(M\) nằm trên đường tròn \(\left( {O;R} \right) \Leftrightarrow OM = R.\) +) \(M\) nằm trong đường tròn \(\left( {O;R} \right) \Leftrightarrow OM < R.\) +) \(M\) nằm ngoài đường tròn \(\left( {O;R} \right) \Leftrightarrow OM > R.\) c) Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn. d) Tính đối xứng của đường tròn. +) Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. +) Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn. 2. Quan hệ đường kính và dây cung. a) So sánh độ dài của đường kính và dây: Trong các dây của đường tròn, dây lớn nhất là đường kính. b) Quan hệ vuông góc giữa đường kính và dây. +) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. +) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy. c) Liên hệ giữa dây và khoảng cách từ tâm đến dây. * Trong một đường tròn: - Hai dây bằng nhau thì cách đều tâm. - Hai dây cách đều tâm thì bằng nhau. * Trong hai dây của một đường tròn: - Dây nào lớn hơn thì dây đó gần tâm hơn . - Dây nào gần tâm hơn thì dây đó lớn hơn. 3. Vị trí tương đối của đường thẳng và đường tròn. Cho đường tròn $\left( {O;R} \right)$ và đường thẳng $a.$ Đặt $d = d\left( {O,a} \right).$ Ta có: 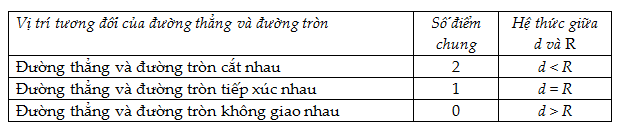 b) Khi đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn. Điểm chung của đường thẳng và đường tròn gọi là tiếp điểm. 4. Dấu hiệu nhận biết tiếp tuyến +) Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm . +) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn. 5. Tính chất hai tiếp tuyến cắt nhau a) Tính chất hai tiếp tuyến cắt nhau Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: +) Điểm đó cách đều hai tiếp điểm. +) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. +) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm. b) Đường tròn nội tiếp tam giác * Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn. * Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác của các góc trong tam giác. c) Đường tròn bàng tiếp tam giác * Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác. * Với một tam giác, có ba đường tròn bàng tiếp. * Tâm của đường tròn bàng tiếp tam giác trong góc \(A\) là giao điểm của hai đường phân giác các góc ngoài tại \(A\) và \(C\) hoặc là giao điểm của phân giác trong góc \(A\) và phân giác ngoài tại \(B\) (hoặc \(C)\) 6. Vị trí tương đối của hai đường tròn a) Tính chất đường nối tâm * Đường nối tâm của hai đường tròn là trục đối xứng của hình gồm cả hai đường tròn đó. * Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm. * Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm. b) Vị trí tương đối của hai đường tròn Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';r} \right)\)\(,R > r\) . Đặt \(OO' = d.\) Ta có: 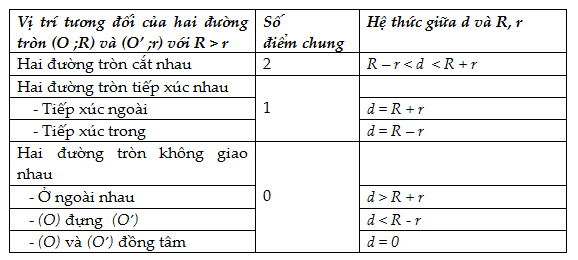 c) Tiếp tuyến chung của hai đường tròn - Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó. - Tiếp tuyến chung ngoài là tiếp tuyến chung không cắt đoạn nối tâm. - Tiếp tuyến chung trong là tiếp tuyến chung cắt đoạn nối tâm.
|













