Lý thuyết Lũy thừa của một số hữu tỉ SGK Toán 7 - Chân trời sáng tạo1. Lũy thừa với số mũ tự nhiên Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... 1. Lũy thừa với số mũ tự nhiên Lũy thừa bậc n của một số hữu tỉ x , kí hiệu xn , là tích của n thừa số x ( n là số tự nhiên lớn hợn 1) xn đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x. x: cơ số n: số mũ Quy ước: x0 = 1 ( x ≠0); x1 = x Chú ý: (x.y)n=xn.yn(xy)n=xnyn + Lũy thừa số mũ chẵn của 1 số hữu tỉ luôn dương + Lũy thừa số mũ lẻ của 1 số hữu tỉ âm luôn âm + Lũy thừa số mũ chẵn của 1 số hữu tỉ dương luôn dương 2. Tích và thương hai lũy thừa cùng cơ số + Khi nhân 2 lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng 2 số mũ xm . xn = xm+n + Khi chia 2 lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi lũy thừa của số chia xm : xn = xm-n (x≠0;m≥n) Ví dụ: 74 . 78 = 74+8 = 712 75 : (-7)2 = 75 : 72 = 75-2 = 73 3. Lũy thừa của lũy thừa Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ. (xm)n = xm.n Ví dụ: [(-3)3]4 = (-3)3.4 = (-3)12 4. Mở rộng Lũy thừa với số mũ nguyên âm của một số hữu tỉ x−n=1xn(x≠0) Ví dụ: 3−2=132 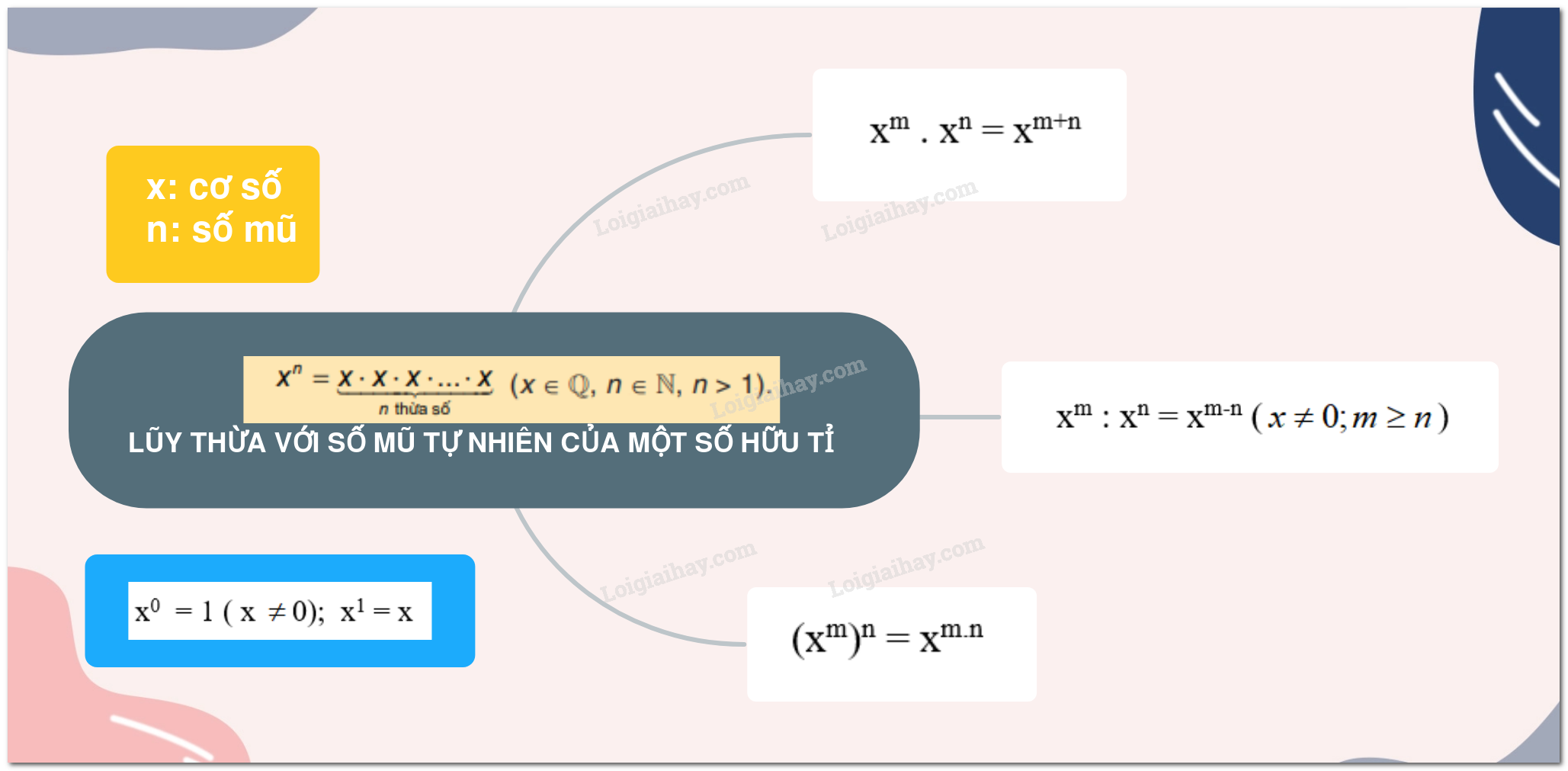
|













