Lý thuyết Khái niệm vectơ - SGK Toán 10 Cánh diềuA. Lý thuyết 1. Khái niệm vectơ Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... A. Lý thuyết 1. Khái niệm vectơ
Xét vectơ →AB: - Điểm đầu: A; điểm cuối: B. - Cách vẽ: Vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B.
- Đường thẳng d qua hai điểm A là giá của vectơ →AB. - Độ dài đoạn thẳng AB là độ dài vectơ →AB, kí hiệu |→AB|.
Khi không cần chỉ rõ điểm đầu và điểm cuối, vectơ còn được kí hiệu là →a,→b,→u,→v,... Độ dài của vectơ →a được kí hiệu là |→a|. 2. Vecto cùng phương, vectơ cùng hướng.
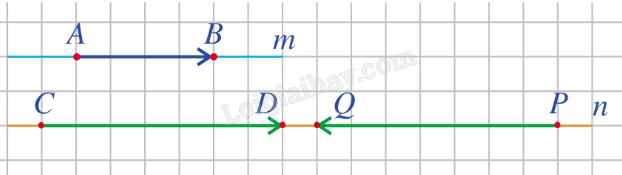
Ví dụ: Các vectơ →AB, →CD và →PQ cùng phương (hình vẽ).
Nhận xét: Nếu hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng. 3. Hai vectơ bằng nhau
Nhận xét: - Hai vectơ →a,→b bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu →a=→b. - Khi cho trước vectơ →a và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho →OA=→a. 4. Vectơ-không
Quy ước: →0 cùng phương, cùng hướng với mọi vectơ và |→0|=0. Có thể coi mọi vectơ-không đều bằng nhau và →0=→AA=→BB=... với mọi điểm A, B,… Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi →AB=→0. 5. Biểu thị một số đại lượng có hướng bằng vectơ Trong vật lí, một số đại lượng như: lực, vận tốc, … là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng có hướng đó, chẳng hạn: Một lực →F tác động lên xe tại điểm đặt A; lực →F có phương nằm ngang, hướng từ trái sang phải và cường độ là 40 N. Ta biểu thị lực →F bằng vectơ →AB như hình vẽ.
B. Bài tập Bài 1: Cho hai điểm phân biệt H, K. Viết các vectơ (có điểm đầu khác điểm cuối) mà hai đầu mút của mỗi vectơ là hai điểm đã cho. Giải: Hai vectơ thoả mãn yêu cầu đề bài là →HK và →KH. Bài 2: Tính độ dài của các vectơ →AB, →CD và →MN ở hình vẽ, biết rằng độ dài cạnh của ô vuông bằng 1 cm.
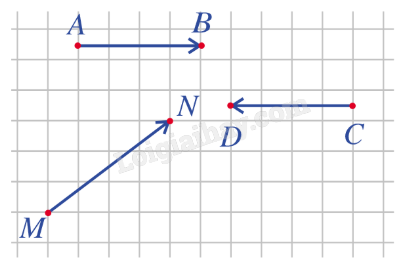
Giải: |→AB|=4 cm, |→CD|=4 cm. |→MN|=√32+42=5 cm. Bài 3: Trong hình vẽ, tìm vectơ cùng hướng với vectơ →AB, ngược hướng với vectơ →AB.
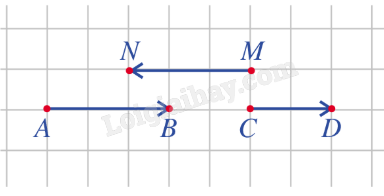
Giải: Vectơ →CD cùng hướng với vectơ →AB, vectơ →MN ngược hướng với vectơ →AB. Bài 4: Cho hình bình hành ABCD.
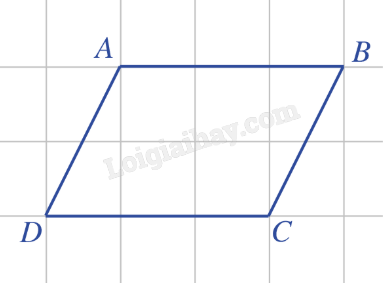
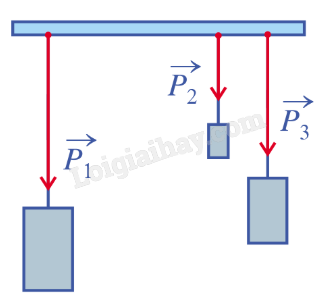
a) Vectơ nào bằng vectơ →AB? b) Vectơ nào bằng vectơ →AD? Giải: a) Vì →AB,→DC cùng hướng và AB = DC nên →AB=→DC. b) Vì →AD,→BC cùng hướng và AD = BC nên →AD=→BC. Bài 5: Khi treo ba vật lên thanh bằng những đoạn dây mảnh, không dãn, khối lượng không đáng kể, mỗi vật sẽ tác dụng lên thanh treo một lực (bằng trọng lượng của vật) như hình vẽ. Nhận xét đặc điểm về phương, hướng của ba vectơ biểu thị ba lực tác dụng lên thanh treo nói trên.
Giải: Ba vectơ →P1,→P2,→P3 biểu thị ba lực tác dụng lên thanh treo là có cùng hướng. 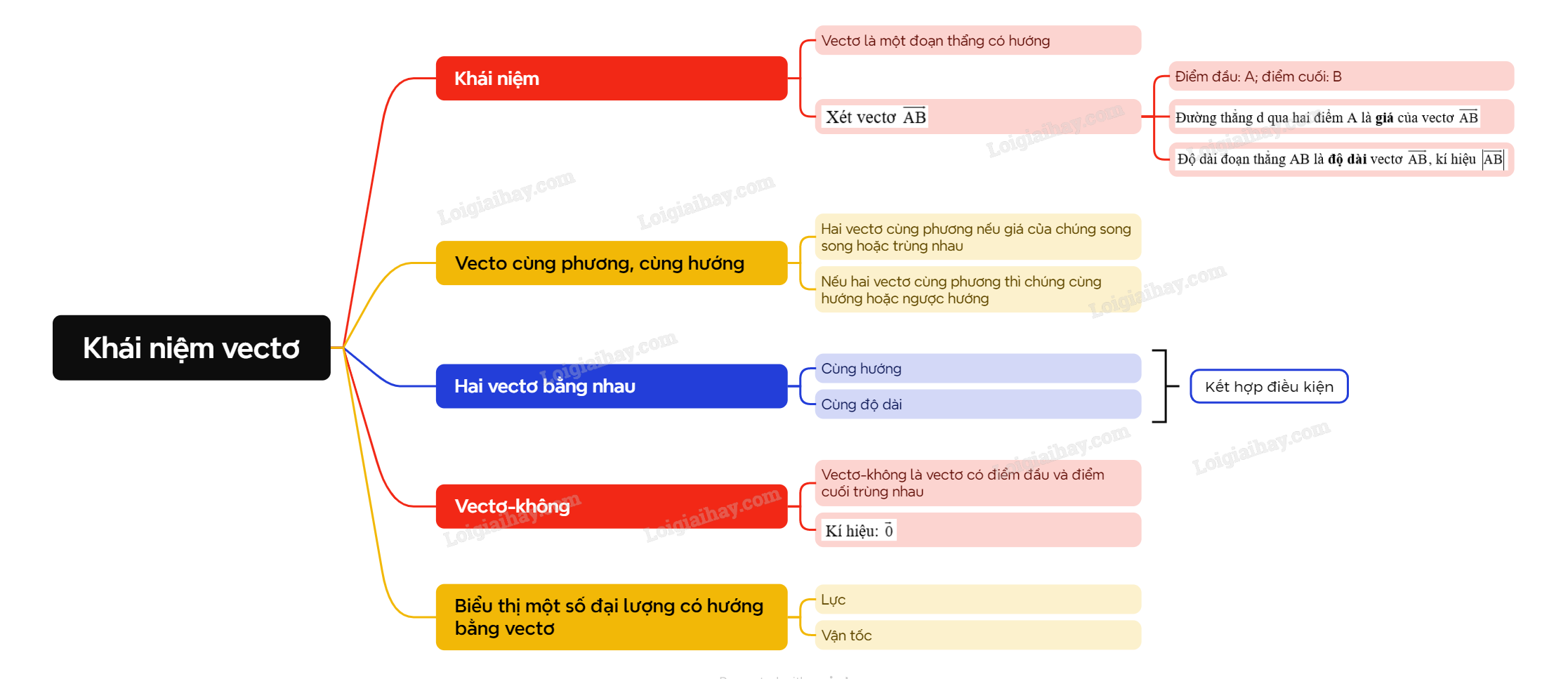
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|