Lý thuyết Hàm số - SGK Toán 10 Kết nối tri thứcA. Lý thuyết 1. Khái niệm hàm số Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... A. Lý thuyết 1. Khái niệm hàm số
Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x),… Chú ý: Khi cho hàm số bằng công thức y = f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. Nhận xét: Một hàm số có thể được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời. 2. Đồ thị của hàm số
3. Sự đồng biến, nghịch biến của hàm số
Chú ý: - Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải. - Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.
B. Bài tập Bài 1 (ví dụ): Bảng dưới đây cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:
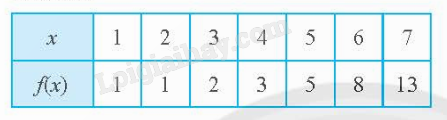
Nếu gọi x là thời điểm, y là nồng độ bụi PM 2.5 thì x là biến số và y là hàm số của x. Đó là hàm số được cho bằng bảng. Bài 2: Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vào thời gian của một vật chuyển động thẳng đều với vận tốc 2 m/s. Tìm tập xác định của hàm số đó. Tính quãng đường vật đi được sau 5 s, 10 s. Giải: Một vật chuyển động thẳng đều với vận tốc v = 2 m/s thì quãng đường đi được S phụ thuộc vào thời gian t (giây) theo công thức S = 2t, trong đó t là biến số, S là hàm số của t. Bài 3: Tìm tập xác định của các hàm số sau: a) \(y = \sqrt {2x - 4} \). b) \(y = \frac{1}{{x - 1}}\). Giải: a) Biểu thức \(\sqrt {2x - 4} \) có nghĩa khi \(2x - 4 \ge 0\), tức là khi \(x \ge 2\). Vậy tập xác định của hàm số đã cho là \(D = [2; + \infty )\). b) Biểu thức \(\frac{1}{{x - 1}}\) có nghĩa khi \(x - 1 \ne 0\), tức là khi \(x \ne 1\). Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}\backslash \{ 1\} \). Bài 4: a) Cho hàm số \(y = f(x) = \frac{1}{8}{x^2}\) xác định trên D = [-3;5] có đồ thị (C) như hình. - Điểm A(4; f(4)) có thuộc đồ thị (C) không? - Lấy điểm B tùy ý trên đồ thị (C). Nêu nhận xét về hoành độ của điểm B. b) Vẽ đồ thị hàm số y = f(x) được cho bởi bảng sau:
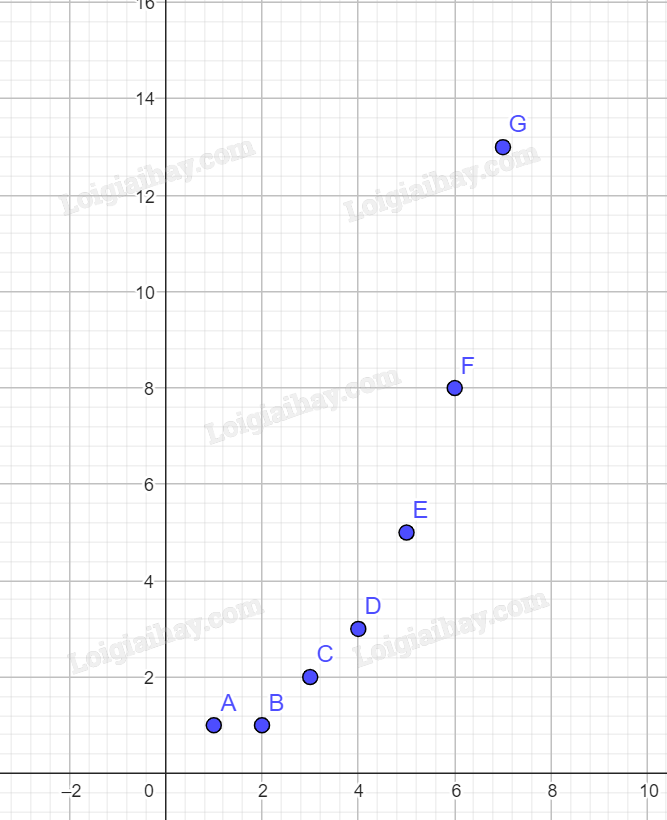
Giải: a) Vì \(4 \in [ - 3;5]\) nên điểm A có hoành độ bằng 4 và tung độ \(y = \frac{1}{8}{.4^2} = 2\) là điểm thuộc đồ thị (C). Khi lấy điểm B tùy ý trên đồ thị (C) thì hoành độ \({x_B}\) của điểm này thuộc tập xác định D, nghĩa là \( - 3 \le {x_B} \le 5\). b) Đồ thị hàm số gồm 7 điểm như hình:
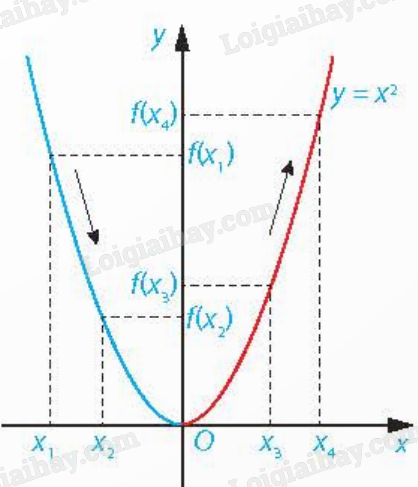
Bài 5: Hàm số \(y = {x^2}\) đồng biến hay nghịch biến trên mỗi khoảng \(( - \infty ;0)\) và \((0; + \infty )\)? Giải: Vẽ đồ thị hàm số \(y = f(x) = {x^2}\) như hình:
- Trên khoảng \(( - \infty ;0)\), đồ thị “đi xuống” từ trái sang phải và với \({x_1},{x_2} \in ( - \infty ;0)\), \({x_1} < {x_2}\) thì \(f({x_1}) > f({x_2})\). Như vậy, hàm số \(y = {x^2}\) nghịch biến trên khoảng \(( - \infty ;0)\). - Trên khoảng \((0; + \infty )\), đồ thị “đi lên” từ trái sang phải và với \({x_3},{x_4} \in (0; + \infty )\), \({x_3} < {x_4}\) thì \(f({x_3}) < f({x_4})\). Như vậy, hàm số \(y = {x^2}\) đồng biến trên khoảng \((0; + \infty )\). 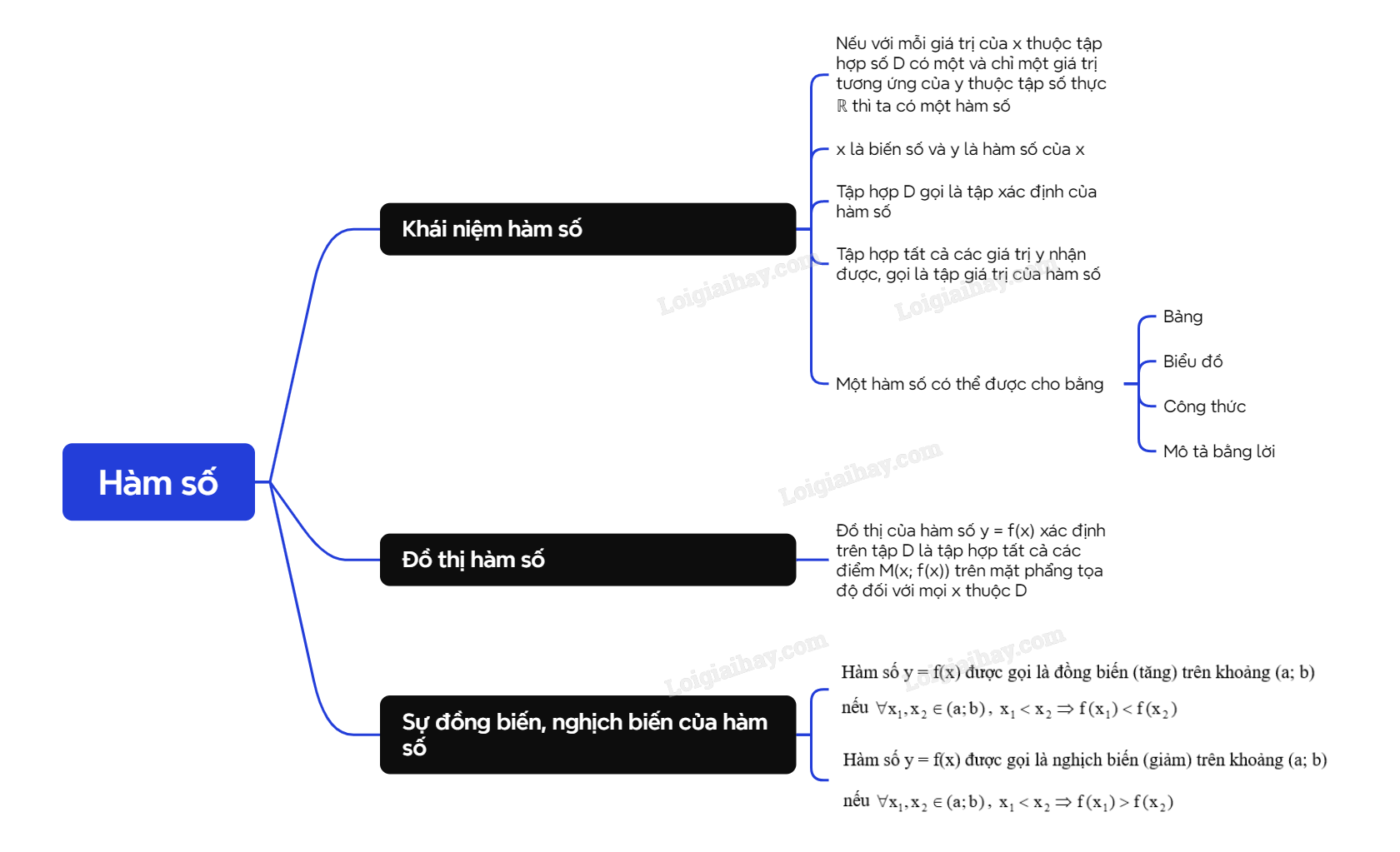
|