Lý thuyết Hàm số bậc hai - SGK Toán 10 Kết nối tri thứcA. Lý thuyết 1. Khái niệm hàm số bậc hai Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... A. Lý thuyết 1. Khái niệm hàm số bậc hai
Nhận xét: Hàm số \(y = a{x^2}\) \((a \ne 0)\) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0. 2. Đồ thị của hàm số bậc hai
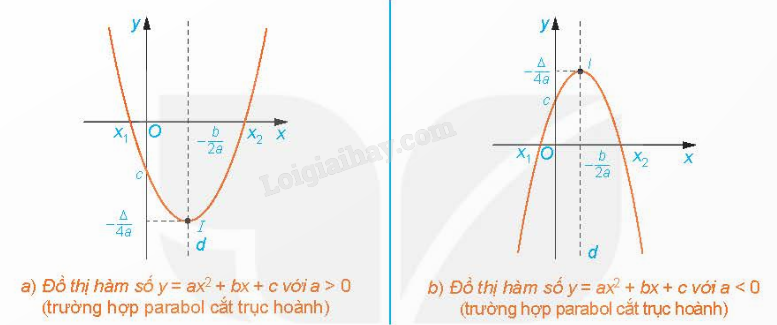
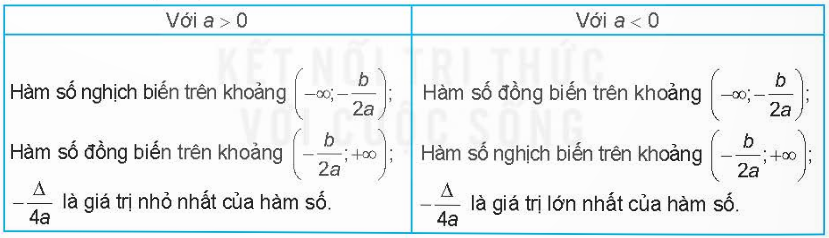
Nhận xét: Từ đồ thị hàm số \(y = a{x^2} + bx + c\) \((a \ne 0)\), ta suy ra tính chất của hàm số \(y = a{x^2} + bx + c\) \((a \ne 0)\):
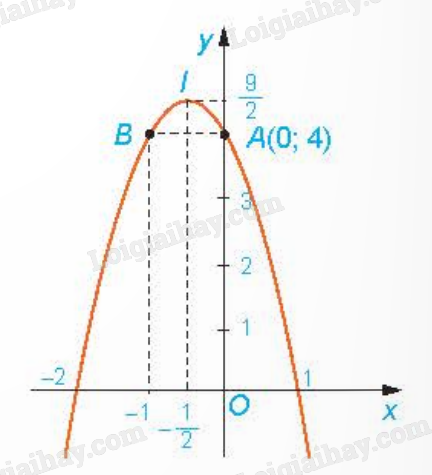
B. Bài tập Bài 1: Hàm số nào dưới đây là hàm số bậc hai? A. \(y = {x^2} + 3{x^2} + 2\) B. \(y = \frac{1}{{{x^2}}}\) C. \(y = - 3{x^2} + 1\) D. \(y = 3{\left( {\frac{1}{x}} \right)^2} - 3\frac{1}{x} - 1\) Giải: Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai với a = -3, b = 0, c = 1. Hàm số thỏa mãn điều kiện \(a \ne 0\) \(( - 3 \ne 0)\) và có tập xác định là \(\mathbb{R}\). Bài 2: a) Vẽ parabol \(y = - 2{x^2} - 2x + 4\). b) Từ đồ thị, hãy tìm khoảng đồng biến, nghịch biến và giá trị lớn nhất của hàm số \(y = - 2{x^2} - 2x + 4\). Giải: a) Ta có a = -2 < 0 nên parabol quay bề lõm xuống dưới. Đỉnh \(I\left( { - \frac{1}{2};\frac{9}{2}} \right)\). Trục đối xứng \(x = - \frac{1}{2}\). Giao điểm của đồ thị với trục Oy là A(0;4). Parabol cắt trục hoành tại điểm có hoành độ là nghiệm của phương trình \( - 2{x^2} - 2x + 4 = 0\), tức là x = 1 và x = -2. Để vẽ đồ thị chính xác hơn, ta có thể lấy thêm điểm đối xứng vói A qua trục đối xứng \(x = - \frac{1}{2}\) là B(-1;4).
b) Từ đồ thị ta thấy: Hàm số \(y = - 2{x^2} - 2x + 4\) đồng biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\), nghịch biến trên \(\left( { - \frac{1}{2}; + \infty } \right)\). Giá trị lớn nhất của hàm số là \(y = \frac{9}{2}\) khi \(x = - \frac{1}{2}\). 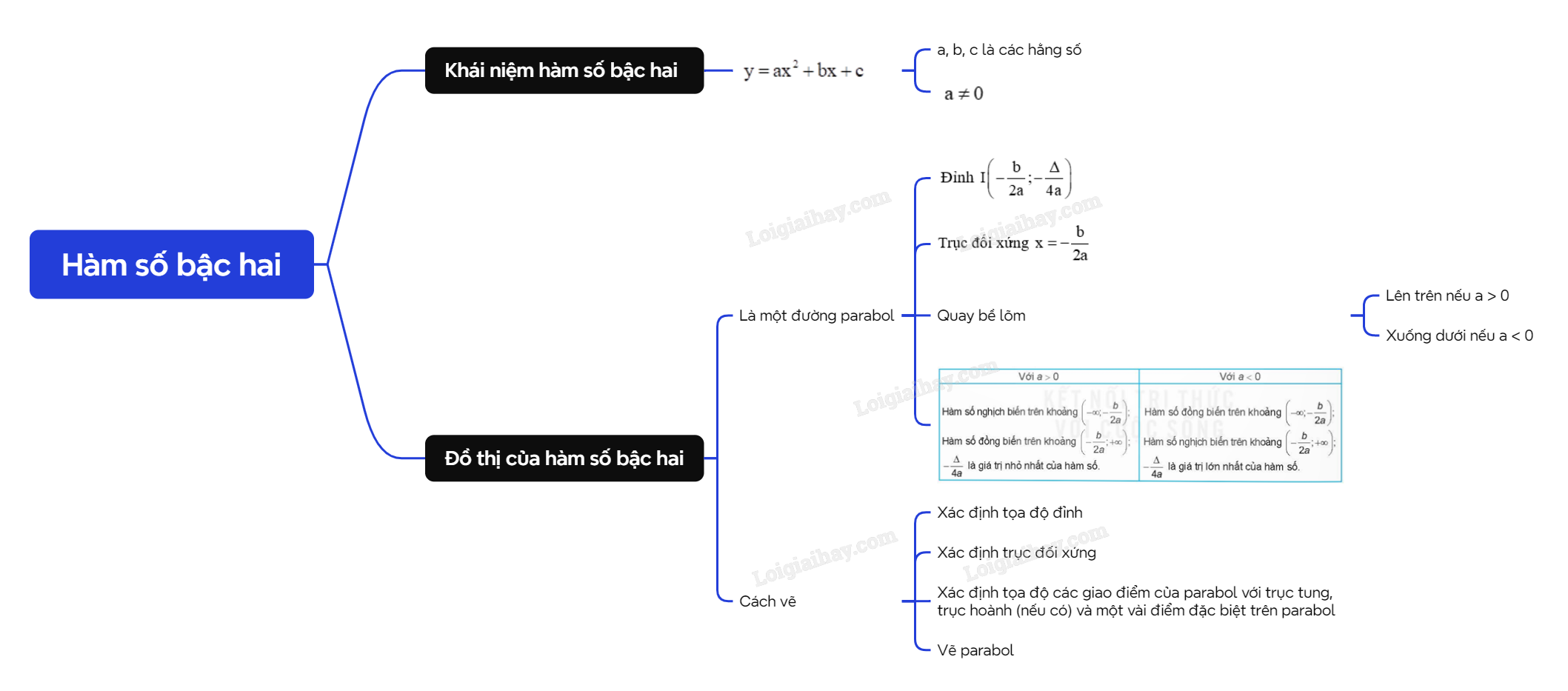
|