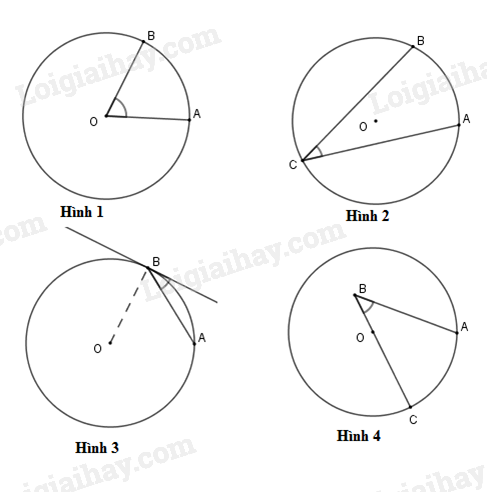
Lý thuyết góc nội tiếp

1. Các kiến thức cần nhớ

Định nghĩa góc nội tiếp

- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

- Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.

Ví dụ: Trên hình $1$, góc $\widehat {ACB}$ là góc nội tiếp chắn cung $AB$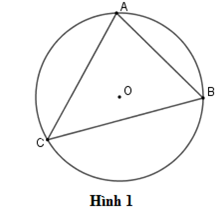

2. Các dạng toán thường gặp

Dạng 1: Chứng minh các tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau

Phương pháp:

Ta thường sử dụng hệ quả

Trong một đường tròn:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng $90^\circ$) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông.

Dạng 2: Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích

Phương pháp:

Ta sử dụng hệ quả để suy ra các góc bằng nhau từ đó chứng minh theo yêu cầu bài toán.

3. Bài tập vận dụng

Câu 1. Hình nào dưới đây biểu diễn góc nội tiếp?

A. Hình $1$ 

B. Hình $2$ 

C. Hình $3$

D. Hình $4$ 

Lời giải chi tiết

Hình $1$ góc $\widehat {BOA}$ là góc ở tâm.

Hình $3$ có $1$ cạnh không phải là dây của đường tròn.

Hình $4$ đỉnh $B$ không nằm trên đường tròn.

Hình $2$ góc $\widehat {BCA}$ là góc nội tiếp chắn cung $AB$.

Đáp án B

Câu 2. Cho đường tròn (O; R). Lấy A, B, C thuộc đường tròn (O; R). Góc nội tiếp ABC chắn cung nào?

A. AB.

B. AC.

C. OC.

D. BC.

Lời giải chi tiết

Góc nội tiếp ABC chắn cung AC.

Đáp án B

Câu 3. Cho hình vẽ (hai đường tròn có tâm là $B,C$ và điểm $B$ nằm trên đường tròn tâm $C$). Biết $\widehat {MAN} = {20^0}.$

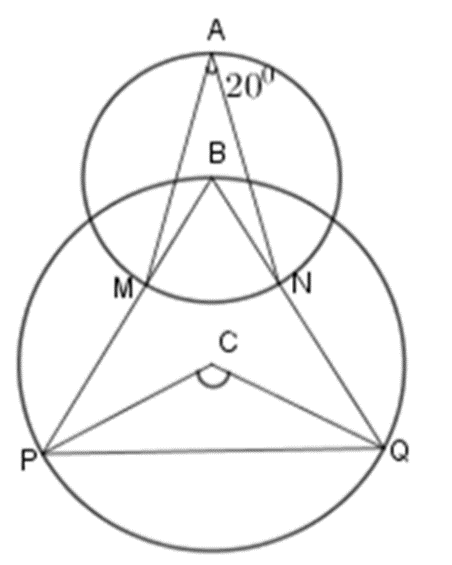
Lời giải chi tiết

Ta nhận thấy $\widehat {MAN}$ nội tiếp đường tròn tâm $B$, chắn cung nhỏ $MN$ của đường tròn $\left( B \right)$ nên $\widehat {MAN} = \dfrac{1}{2}\widehat {MBN} = {20^0} \Rightarrow \widehat {MBN} = {40^0} \Rightarrow \widehat {PBQ} = {40^0}.$

Ta lại có $\widehat {PBQ}$ là góc nội tiếp đường tròn tâm $C$ và $\widehat {PCQ}$ là góc ở tâm của $\left( C \right)$ nên

$\widehat {PBQ} = \dfrac{1}{2}\widehat {PCQ} \Rightarrow \widehat {PCQ} = 2\widehat {PBQ} = {80^0}.$

Vậy $\widehat {PCQ} = {80^0}.$

Câu 4. Cho hình vẽ bên. Mệnh đề nào sau đây là sai.

A. $\widehat {AMB} = \widehat {ANB}$

B. $\widehat {AMB} = \dfrac{1}{2}\widehat {AOB}$

C. $\widehat {ANB} = \dfrac{1}{2}\widehat {AOB}$

D. $\widehat {AMB} = \widehat {ANB} = \widehat {AOB}$

Lời giải chi tiết

Ta có $\widehat {AMB} = \widehat {ANB}$ vì hai góc nội tiếp cùng chắn cung $AB.$

Ta lại có $\widehat {AMB} = \dfrac{1}{2}\widehat {AOB},\widehat {\,\,ANB} = \dfrac{1}{2}\widehat {AOB}$ ( mối liên hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung $AB)$

Đáp án D

Câu 5. Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Chứng minh $AH.AD = AC.AB$.

Lời giải chi tiết

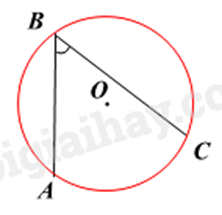
Xét $\left( O \right)$ có $\widehat {ACB} = \widehat {ADB}$  (hai góc nội tiếp cùng chắn cung $AB$ ); $\widehat {ABD} = 90^\circ$  (góc nội tiếp chắn nửa đường tròn)

Xét $\Delta ACH$ và $\Delta ADB$ có:

$\widehat {ACB} = \widehat {ADB}$

$\widehat {AHC} = \widehat {ABD} (= 90^\circ)$

Nên $\Delta ACH \backsim \Delta ADB\left( {g - g} \right)$

Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}}$

Do đó $AH.AD = AC.AB$.

Câu 6. Cho đường  tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$.  Chứng minh $A{B^2} = AE.AD$.

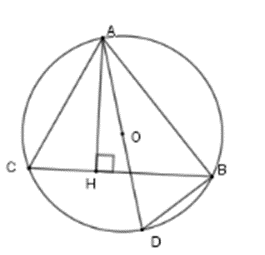
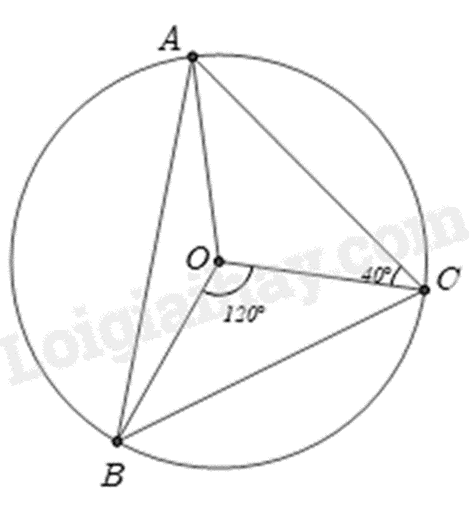
Lời giải chi tiết

Xét $\left( O \right)$ có $\widehat {AEB} = \widehat {ABC}$ (hai góc nội tiếp chắn hai cung bằng nhau $AB = AC$ )

Xét $\Delta ABD$ và $\Delta AEB$ có $\widehat A$ chung và $\widehat {AEB} = \widehat {ABC}$ (cmt) nên $\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD$

Câu 7. Cho tam giác ABC nội tiếp đường tròn (O). Biết $\widehat {BOC} = 120^\circ$ và $\widehat {OCA} = 40^\circ$. Tính số đo góc BAO.

Lời giải chi tiết

Vì tam giác AOC cân nên $\widehat {OAC} = \widehat {OCA} = 40^\circ$

Vì tam giác ABC nội tiếp đường tròn (O) nên $\widehat {BAC}$ là góc nội tiếp chắn cung BC. Mà $\widehat {BOC}$ là góc ở tâm chắn cung BC nên $\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}.120^\circ  = 60^\circ$.

Mà $\widehat {BAO} + \widehat {OAC} = \widehat {BAC}$ nên ta có:

$\widehat {BAO} = \widehat {BAC} - \widehat {OAC} = 60^\circ  - 40^\circ  = 20^\circ$.