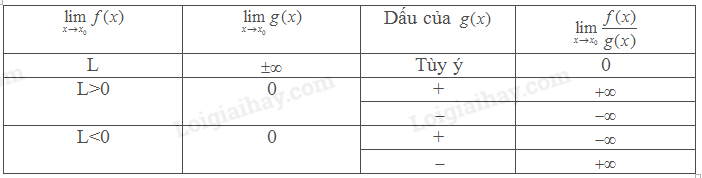
Lý thuyết Giới hạn của hàm số - SGK Toán 11 Kết nối tri thức

1. Giới hạn hữu hạn của hàm số tại một điểm

Giả sử (a;b) là một khoảng chứa điểm ${x_0}$và hàm số $y = f(x)$xác định trên khoảng (a;b), có thể trừ điểm ${x_0}$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x$ dần tới ${x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì, ${x_n} \in \left( {a;b} \right)$,${x_n} \ne {x_0}$ và ${x_n} \to {x_0}$, ta có$f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$hay $f(x) \to L$, khi ${x_n} \to {x_0}$.

*Quy tắc tính giới hạn của hàm số tại một điểm

a, Nếu $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$và $\mathop {\lim }\limits_{x \to {x_0}} g(x) = M$thì

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M$

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M$

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)$

b, Nếu $f(x) \ge 0$với mọi $x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}$ và $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$ thì $L \ge 0$và $\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)}  = \sqrt L$.

2. Giới hạn một bên

Cho hàm số $y = f(x)$xác định trên khoảng $\left( {{x_0};b} \right)$. Ta nói số L là giới hạn bên phải của $f(x)$khi $x \to {x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn ${x_0} < {x_n} < b$ và ${x_n} \to {x_0}$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L$.

Cho hàm số $y = f(x)$xác định trên khoảng $\left( {a;{x_0}} \right)$. Ta nói số L là giới hạn bên trái của khi $x \to {x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn $a < {x_n} < {x_0}$ và ${x_n} \to {x_0}$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L$.

3. Giới hạn hữu hạn của hàm số tại vô cực

Cho hàm số $y = f(x)$xác định trên khoảng $\left( {a; + \infty } \right)$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x \to  + \infty$ nếu với dãy số $\left( {{x_n}} \right)$bất kì ${x_n} > a$ và ${x_n} \to  + \infty$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } f(x) = L$ hay $f(x) \to L$ khi $x \to  + \infty$.

Cho hàm số $y = f(x)$xác định trên khoảng $\left( { - \infty ;b} \right)$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x \to  - \infty$ nếu với dãy số $\left( {{x_n}} \right)$bất kì ${x_n} < b$ và ${x_n} \to  - \infty$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to  - \infty } f(x) = L$ hay $f(x) \to L$ khi $x \to  - \infty$.

* Nhận xét:

Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.

Với c là hằng số, $\mathop {\lim }\limits_{x \to  + \infty } c = c$, $\mathop {\lim }\limits_{x \to  - \infty } c = c$.

Với k là một số nguyên dương, ta có: $\mathop {\lim }\limits_{x \to  + \infty } (\frac{1}{{{x^k}}}) = 0,\mathop {\lim }\limits_{x \to  - \infty } (\frac{1}{{{x^k}}}) = 0$.

4. Giới hạn vô cực của hàm số tại một điểm

a, Giới hạn vô cực

- Giả sử (a;b) là một khoảng chứa ${x_0}$và hàm số $y = f(x)$xác định trên khoảng $\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}$. Ta nói hàm số $f(x)$có giới hạn là $+ \infty$khi $x$ dần tới ${x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì, $\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}$ và ${x_n} \to {x_0}$, ta có$f({x_n}) \to  + \infty$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}} f(x) =  + \infty$.

Ta nói hàm số $f(x)$có giới hạn $- \infty$khi $x \to {x_0}$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}} f(x) =  - \infty$, nếu $\mathop {\lim }\limits_{x \to {x_0}} \left[ { - f(x)} \right] =  + \infty$.

- Cho hàm số $y = f(x)$xác định trên khoảng $\left( {{x_0};b} \right)$. Ta nói hàm số $f(x)$có giới hạn $+ \infty$ khi $x \to {x_0}$ về bên phải nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn ${x_0} < {x_n} < b$ và ${x_n} \to {x_0}$ta có $f({x_n}) \to  + \infty$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) =  + \infty$.

Cho hàm số $y = f(x)$xác định trên khoảng $\left( {a;{x_0}} \right)$. Ta nói hàm số $f(x)$có giới hạn $+ \infty$ khi $x \to {x_0}$ về bên trái nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn $a < {x_n} < {x_0}$ và ${x_n} \to {x_0}$ta có $f({x_n}) \to  + \infty$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) =  + \infty$.

Các giới hạn một bên$\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) =  - \infty$, $\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) =  - \infty$ được định nghĩa tương tự.

b, Một số quy tắc tính giới hạn vô cực

*Giới hạn của tích$\mathop {\lim }\limits_{x \to {x_0}} f(x).g(x)$

*Giới hạn của thương $\frac{{f(x)}}{{g(x)}}$