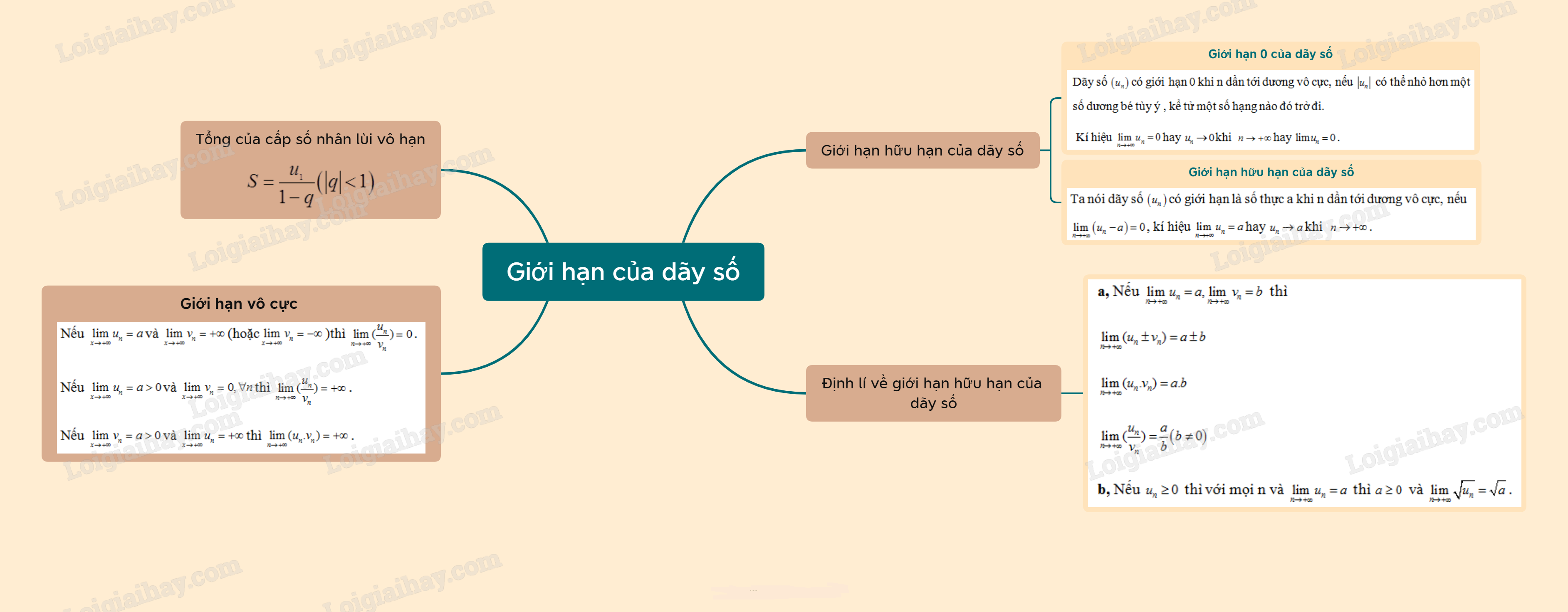
Lý thuyết Giới hạn của dãy số - SGK Toán 11 Kết nối tri thức

1, Giới hạn hữu hạn của dãy số

Ta nói dãy số $\left( {{u_n}} \right)$ có giới hạn 0 khi n dần tới dương vô cực, nếu $\left| {{u_n}} \right|$ có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi, kí hiệu $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = 0$ hay ${u_n} \to 0$ khi  $n \to  + \infty$.

Ta nói dãy số $\left( {{u_n}} \right)$ có giới hạn là số thực a khi n dần tới dương vô cực, nếu $\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n} - a} \right) = 0$, kí hiệu $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a$ hay ${u_n} \to a$ khi  $n \to  + \infty$.

* Chú ý: Nếu ${u_n} = c$ (c là hằng số) thì $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = c$

2. Định lí về giới hạn hữu hạn của dãy số

a, Nếu $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to  + \infty } {v_n} = b$ thì

$\mathop {\lim }\limits_{n \to  + \infty } ({u_n} \pm {v_n}) = a \pm b$

$\mathop {\lim }\limits_{n \to  + \infty } ({u_n}.{v_n}) = a.b$

$\mathop {\lim }\limits_{n \to  + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)$

b, Nếu ${u_n} \ge 0$ thì với mọi n và $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a$ thì $a \ge 0$ và $\mathop {\lim }\limits_{n \to  + \infty } \sqrt {{u_n}}  = \sqrt a$.

3. Tổng của cấp số nhân lùi vô hạn

$S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)$

4. Giới hạn vô cực của dãy số

Dãy số $\left( {{u_n}} \right)$ được gọi là có giới hạn $+ \infty$khi $n \to  + \infty$nếu ${u_n}$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  + \infty$ hay ${u_n} \to  + \infty$ khi $n \to  + \infty$.

Dãy số $\left( {{u_n}} \right)$ được gọi là có giới hạn $- \infty$ khi $n \to  + \infty$ nếu $\mathop {\lim }\limits_{x \to  + \infty } \left( { - {u_n}} \right) =  + \infty$, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  - \infty$ hay ${u_n} \to  - \infty$ khi $n \to  + \infty$.

*Quy tắc:

Nếu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} = a$ và $\mathop {\lim }\limits_{x \to  + \infty } {v_n} =  + \infty$(hoặc$\mathop {\lim }\limits_{x \to  + \infty } {v_n} =  - \infty$) thì $\mathop {\lim }\limits_{n \to  + \infty } (\frac{{{u_n}}}{{{v_n}}}) = 0$.

Nếu $\mathop {\lim }\limits_{x \to  + \infty } {u_n} = a > 0$ và $\mathop {\lim }\limits_{x \to  + \infty } {v_n} = 0,\forall n$ thì $\mathop {\lim }\limits_{n \to  + \infty } (\frac{{{u_n}}}{{{v_n}}}) =  + \infty$.

Nếu $\mathop {\lim }\limits_{x \to  + \infty } {v_n} = a > 0$ và $\mathop {\lim }\limits_{x \to  + \infty } {u_n} =  + \infty$ thì $\mathop {\lim }\limits_{n \to  + \infty } ({u_n}.{v_n}) =  + \infty$.