Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180. Định lí cosin và định lí sin trong tam giác - SGK Toán 10 Cánh diều

I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180

1. Giá trị lượng giác của một góc từ 0 đến 180

+) Với mỗi góc $\alpha ({0^o} \le \alpha {\rm{\;}} \le {180^o})$ có duy nhất điểm $M({x_0};{y_0})$ trên nửa đường tròn đơn vị để $\widehat {xOM} = \alpha .$Khi đó:

$\sin \alpha {\rm{\;}} = {y_0}$ là tung độ của M

$\cos \alpha {\rm{\;}} = {x_0}$ là hoành độ của M

$\tan \alpha {\rm{\;}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha {\rm{\;}} \ne {90^o})$

$\cot \alpha {\rm{\;}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha {\rm{\;}} \ne {0^o},\alpha {\rm{\;}} \ne {180^o})$

 2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

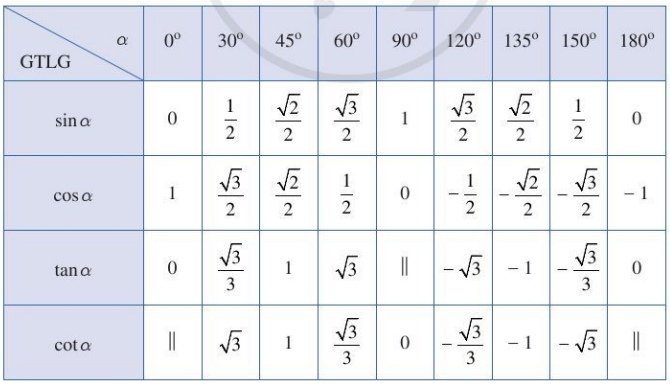
 3. Các giá trị lượng giác của một số góc đặc biệt

II. ĐỊNH LÍ COSIN

1.  Định lí cosin

Trong tam giác ABC:

$\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc\cos A}\\{{b^2} = {c^2} + {a^2} - 2ca\cos B}\\{{c^2} = {a^2} + {b^2} - 2ab\cos C}\end{array}$          

2.  Hệ quả

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$

 III. ĐỊNH LÍ SIN

1.  Định lí sin

Trong tam giác ABC: $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.$

(R là bán kính đường tròn ngoại tiếp tam giác ABC)

2.  Hệ quả

Hệ quả

$a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C$

$\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.$