Lý thuyết đa giác - đa giác đều1. Khái niệm đa giác I. Các kiến thức cần nhớ 1. Đa giác lồi Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó. Ví dụ: Tứ giác \(ABCD\) ở hình 1 là đa giác lồi. Hình 2 không phải đa giác lồi. 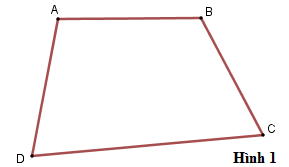 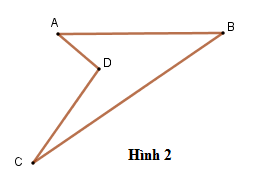 2. Đa giác đều Định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. 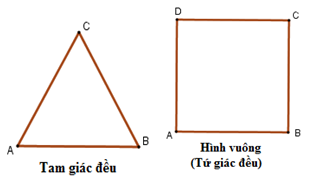  Chú ý: + Đa giác \(n\) đỉnh \(\left( {n \ge 3} \right)\) được gọi là hình \(n\)- giác hay hình \(n\)-cạnh. + Tổng các góc của đa giác $n$ cạnh bằng $\left( {n - 2} \right).180^\circ $ . + Mỗi góc của đa giác đều $n$ cạnh bằng \(\dfrac{{\left( {n - 2} \right).180^\circ }}{n}\). + Số các đường chéo của đa giác lồi $n$ cạnh bằng \(\dfrac{{n\left( {n - 3} \right)}}{2}\) . II. Các dạng toán thường gặp Dạng 1: Tính số đo các góc trong ngoài của đa giác đều,tìm các cạnh các đường chéo của đa giác, chứng minh một đa giác là đều,… Phương pháp: Ta thường sử dụng các kiến thức sau + Đa giác \(n\) đỉnh \(\left( {n \ge 3} \right)\) được gọi là hình \(n\)- giác hay hình \(n\)-cạnh. + Tổng các góc của đa giác $n$ cạnh bằng $\left( {n - 2} \right).180^\circ $ . + Mỗi góc của đa giác đều $n$ cạnh bằng \(\dfrac{{\left( {n - 2} \right).180^\circ }}{n}\). + Số các đường chéo của đa giác $n$ cạnh bằng \(\dfrac{{n\left( {n - 3} \right)}}{2}\) .  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
