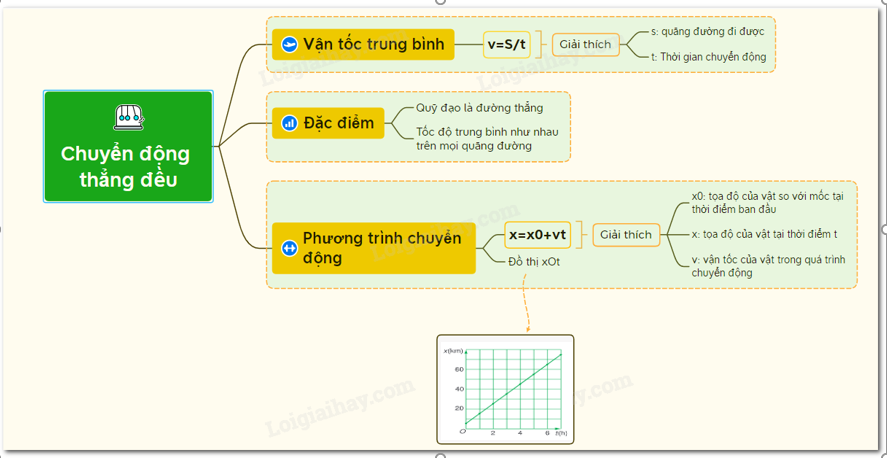
Lý thuyết chuyển động thẳng đều

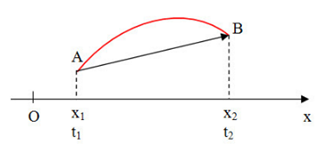CHUYỂN ĐỘNG THẲNG ĐỀU

- Độ dời không phụ thuộc vào hình dạng của quỹ đạo chuyển động mà chỉ phụ thuộc vào vị trí điểm đầu và vị trí điểm cuối

- Véctơ \(\overrightarrow {AB} \) gốc tại điểm A hướng về điểm B gọi là véctơ độ dời

- Định nghĩa:

+ Vận tốc trung bình

\({v_{tb}} = \frac{{\Delta x}}{{\Delta t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}\)

Với x₁, x₂ là tọa độ của chất điểm tại các thời điểm t₁và t₂.

Vận tốc trung bình có phương, chiều trùng với phương, chiều của véc tơ độ dời.

Chúng ta phân biệt giữa vận tốc trung bình với tốc độ trung bình (Học từ lớp 7)

Tốc độ trung bình = \(\frac{{{S_1} + {S_2} + ...{S_n}}}{{{t_1} + {t_2} + ....{t_n}}}\)

+ Vận tốc tức thời

Vận tốc tức thời tại một thời điểm t đặc trưng cho chiều và độ nhanh chậm của chuyển động tại thời điểm đó.

Khi  \(\Delta t \to 0\) thì    \(\frac{{\Delta x}}{{\Delta t}} \simeq \frac{{\Delta s}}{{\Delta t}}\)

Tức là vận tốc tức thời luôn bằng tốc độ tức thời.

Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ  đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

-  Đặc điểm của chuyển động thẳng đều

       + Quỹ đạo chuyển động: là một đường thẳng

       + Vận tốc chuyển động: không đổi

       + Gia tốc chuyển động: bằng không

- Công thức liên hệ giữa v - s - t của chuyển động thẳng đều

Trong đó:

       + v: vận tốc của chuyển động thẳng đều

       + s: quãng đường đi được

       + t: thời gian đi hết quãng đường s

Trong đó:

       + x: tọa độ của vật tại thời điểm t

       + x₀: tọa độ của vật tại thời điểm ban đầu t₀

       + v: vận tốc tức thời (gọi tắt là vận tốc) của vật

       + t₀: gốc thời gian

+ Để đơn giản: ta chọn gốc thời gian t₀ = 0

+ Quãng đường vật đi được sau khoảng thời gian \(\Delta t\) : \(s = \left| v \right|\Delta t\)

+ Nếu vật chuyển động thẳng và không đổi chiều ta có: \(\Delta x = x - {x_0} = s\)(độ dời bằng quãng đường)

+ Dấu của vận tốc phụ thuộc vào chiều dương mà ta chọn, nếu vật chuyển động cùng chiều dương \(v > 0\) , vật chuyển động ngược chiều dương \(v < 0\).

1. Đồ thị tọa độ theo thời gian (x - t)

\(x = {x_0} + vt\) dạng đồ thị giống đồ thị của hàm số \(y = ax + b\)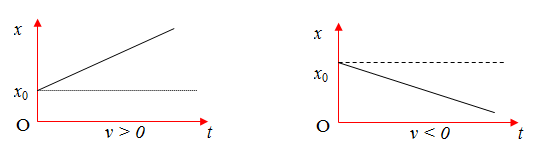

Độ dốc của đường thẳng:

\(tag\alpha  = \dfrac{{x - {x_0}}}{t} = v\)

2. Đồ thị vận tốc theo thời gian (v - t)

Trong chuyển động thẳng đều, vận tốc không thay đổi \(v = {v_0}\)

Đồ thị biểu diễn vận tốc theo thời gian là một đường thẳng song song với trục thời gian.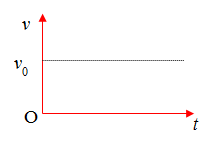

Sơ đồ tư duy về chuyển động thẳng đều - Vật lí 10