Lý thuyết chia đa thức một biến đã sắp xếpTa trình bày phép chia tương tự như cách chia các số tự nhiên. 1. Các kiến thức cần nhớ Chia đa thức một biến đã sắp xếp - Muốn chia đa thức một biến $A$ cho đa thức một biến$B \ne 0$ , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên. - Với hai đa thức tùy ý $A$ và $B$ của một biến $\left( {B \ne 0} \right)$, tồn tại duy nhất hai đa thức $Q$ và $R$ sao cho $A = B.Q + R$ Trong đó $R = 0$ hoặc bậc của $R$ thấp hơn bậc của $B.$ + Nếu $R = 0$ thì phép chia $A$ cho $B$ là phép chia hết. + Nếu $R \ne 0$ thì phép chia $A$ cho $B$ là phép chia có dư. Ví dụ 1:  Ta viết lại \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right) = 3{x^2} - 5x + 2\). Nhận thấy số dư \(R = 0\) nên đây là phép chia hết. Ví dụ 2: 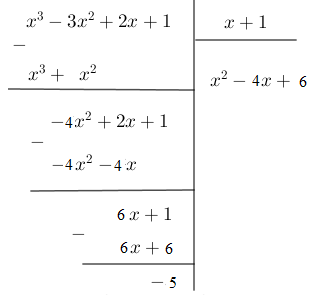 Ta viết lại \({x^3} - 3{x^2} + 2x + 1 = \left( {x + 1} \right)\left( {{x^2} - 4x + 6} \right) - 5\) . Vì \(R = - 5 \ne 0\) nên đây là phép chia có dư. 2. Các dạng toán thường gặp Dạng 1: Tìm thương, số dư của phép chia đa thức một biến đã sắp xếp Phương pháp: Muốn chia đa thức một biến $A$ cho đa thức một biến$B \ne 0$ , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên. Dạng 2: Xác định hằng số \(a,b\) sao cho phép chia cho trước là phép chia hết. Phương pháp: Sử dụng tính chất phép chia hết có số dư \(R = 0\) để tìm \(a,b\) . Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
|



















