Bài 7. Gia tốc - Chuyển động thẳng biến đổi đều trang 19, 20, 21, 22, 23, 24, 25 SBT Vật lí 10 Chân trời sáng tạoTrong chuyển động thẳng biến đổi đều, gia tốc Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
Trắc nghiệm 7.1 Trong chuyển động thẳng biến đổi đều, gia tốc A. có giá trị bằng 0. B. là một hằng số khác 0. C. có giá trị biến thiên theo thời gian. D. chỉ thay đổi hướng chứ không thay đổi về độ lớn. Phương pháp giải: Vận dụng kiến thức về gia tốc trong chuyển động thẳng biến đổi đều. Lời giải chi tiết: Đại lượng đặc trưng cho độ biến thiên của vận tốc theo thời gian được gọi là gia tốc, Trong chuyển động thẳng biến đổi đều, gia tốc trung bình (gọi tắt là gia tốc) là một hằng số khác 0. => Chọn B Trắc nghiệm 7.2 Chọn từ/cụm từ thích hợp trong bảng dưới đây để điền vào chỗ trống.
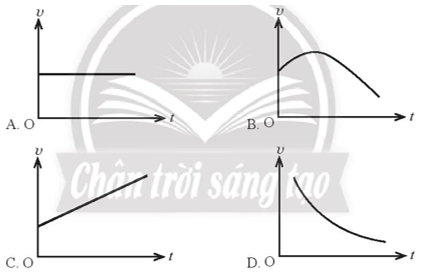
Gia tốc là đại lượng đặc trưng cho độ biến thiên của (1) … theo (2) … Gia tốc là một đại lượng (3) …, có đơn vị trong hệ SI là (4) … Gia tốc tức thời tại một thời điểm có giá trị bằng (5) … của tiếp tuyến với đường đồ thị (6) … tại thời điểm đó. (7) … của vật trong khoảng thời gian từ t1 đến t2 được xác định bằng phần (8) … giới hạn bởi các đường v(t), v = 0, t = t1, t = t2 trong đồ thị (v – t). Phương pháp giải: Vận dụng kiến thức về định nghĩa gia tốc. Lời giải chi tiết: Gia tốc là đại lượng đặc trưng cho độ biến thiên của (1) vận tốc theo (2) thời gian. Gia tốc là một đại lượng (3) có hướng, có đơn vị trong hệ SI là (4) m/s2. Gia tốc tức thời tại một thời điểm có giá trị bằng (5) độ dốc của tiếp tuyến với đường đồ thị (6) (v – t) tại thời điểm đó. (7) Độ dịch chuyển của vật trong khoảng thời gian từ t1 đến t2 được xác định bằng phần (8) diện tích giới hạn bởi các đường v(t), v = 0, t = t1, t = t2 trong đồ thị (v – t). Trắc nghiệm 7.3 Một xe máy đang đứng yên, sau đó khởi động và bắt đầu tăng tốc. Nếu chọn chiều dương là chiều chuyển động của xe, nhận xét nào sau đây là đúng? A. a > 0, v > 0. B. a < 0, v < 0. C. a > 0, v < 0. D. a < 0, v > 0. Phương pháp giải: Vận dụng kiến thức về dấu của a và v trong chuyển động nhanh dần. Lời giải chi tiết: Vì chọn chiều dương là chiều chuyển động => v > 0. Vì xe đang bắt đầu tăng tốc => chuyển động nhanh dần => a > 0. => Chọn A Trắc nghiệm 7.4 Trong các đồ thị vận tốc – thời gian dưới đây, đồ thị nào mô tả chuyển động thẳng biến đổi đều?
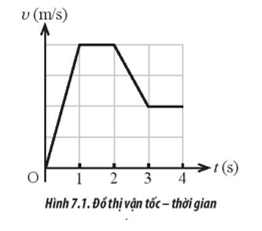
Phương pháp giải: Vận dụng kiến thức về dạng đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều. Lời giải chi tiết: Trong chuyển động thẳng biến đổi đều, ta có công thức vận tốc của vật là: \(v = {v_0} + at\,\left( {a \ne 0} \right)\) trong đó v là vận tốc tại thời điểm t, v0 là vận tốc vật lúc đầu, a là gia tốc chuyển động. => Đồ thị (v – t) có dạng là một đường thẳng không song song với trục hoành (đồ thị A là đồ thị (v – t) của chuyển động thẳng đều) => Chọn C Trắc nghiệm 7.5 Trong các phương trình mô tả vận tốc v (m/s) của vật theo thời gian t (s) dưới đây, phương trình nào mô tả chuyển động thẳng biến đổi đều? A. v =7. B. v = 6t2 + 2t – 2. C. v = 5t – 4. D. v = 6t2 – 2. Phương pháp giải: Trong chuyển động thẳng biến đổi đều, ta có công thức vận tốc của vật là: \(v = {v_0} + at\,\left( {a \ne 0} \right)\)trong đó v là vận tốc tại thời điểm t, v0 là vận tốc vật lúc đầu, a là gia tốc chuyển động. Lời giải chi tiết: Trong tất cả các đáp án chỉ có phương trình vận tốc ở đáp án C có dạng: \(v = {v_0} + at\,\left( {a \ne 0} \right)\). Với a = 5 m/s2, v0 = -4 m/s. => Chọn C Trắc nghiệm 7.6 Quan sát đồ thị (v – t) trong Hình 7.1 của một vật đang chuyển động thẳng và cho biết quãng đường vật đi được trong khoảng thời gian nào là lớn nhất?
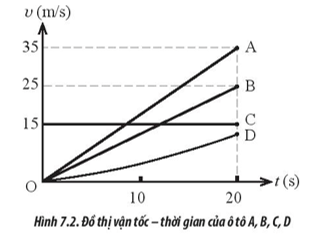
A. Trong khoảng thời gian từ 0 đến 1 s. B. Trong khoảng thời gian từ 1 s đến 2 s. C. Trong khoảng thời gian từ 2 s đến 3 s. D. Trong khoảng thời gian từ 3 s đến 4 s. Phương pháp giải: Độ dịch chuyển của vật trong khoảng thời gian từ t1 đến t2 được xác định bằng phần diện tích giới hạn bởi các đường v(t), v = 0, t = t1, t = t2 trong đồ thị (v – t). Lời giải chi tiết: Quãng đường vật đi được trong khoảng thời gian từ 0 đến 1 s là: \({S_1} = \frac{1}{2}.1.4 = 2\) Quãng đường vật đi được trong khoảng thời gian từ 1 s đến 2 s là: \({S_2} = 1.4 = 4\) Quãng đường vật đi được trong khoảng thời gian từ 2 s đến 3 s là: \({S_3} = \frac{1}{2}.1.2 + 1.2 = 3\) Quãng đường vật đi được trong khoảng thời gian từ 3 s đến 4 s là: \({S_4} = 1.2 = 2\) => Quãng đường vật đi được trong khoảng thời gian từ 1 s đến 2 s là lớn nhất. => Chọn B Trắc nghiệm 7.7 Xét hai xe A và B chuyển động cùng nhau vào hầm Thủ Thiêm dài 1490 m. Xe A chuyển động với tốc độ ban đầu trước khi vào hầm là 60 km/h và chuyển động chậm dần đều với gia tốc 144 km/h2, xe B chuyển động chậm dần đều với gia tốc 120 km/h2 từ lúc bắt đầu chạy vào hầm với tốc độ 55 km/h. Nhận định nào sau đây là đúng về thời gian chuyển động của hai xe trong hầm? A. Hai xe đi hết hầm Thủ Thiêm cùng một khoảng thời gian. B. Xe B ra khỏi hầm trước xe A. C. Xe A ra khỏi hầm trước xe B. D. Dữ liệu bài toán không đủ kết luận. Phương pháp giải: Vận dụng kiến thức về mối liên hệ giữa quãng đường, gia tốc, vận tốc và thời gian của vật đi trong quá trình chuyển động thẳng biến đổi đều: \(S = {v_0}t + \frac{1}{2}a{t^2}\) Lời giải chi tiết: Đổi 1490 m = 1,49 km. Từ công thức \(S = {v_0}t + \frac{1}{2}a{t^2}\) ta tính được thời gian 2 xe đi hết hầm Thủ Thiêm như sau: Thay số vào ta có: Xe A: \(1,49 = 60t + \frac{1}{2}.\left( { - 144} \right){t^2}\) (1); Xe B: \(1,49 = 55t + \frac{1}{2}.\left( { - 120} \right){t^2}\) (2) Giải phương trình (1) ta được: Thời gian xe A đi hết hầm Thủ Thiêm là: t = 0,026 h Giải phương trình (2) ta được: Thời gian xe B đi hết hầm Thủ Thiêm là: t = 0,028 h => Xe A ra khỏi hầm trước xe B. => Chọn C Trắc nghiệm 7.8 Hình 7.2 mô tả đồ thị (v – t) của bốn xe ô tô A, B, C, D. Nhận định nào sau đây là đúng?
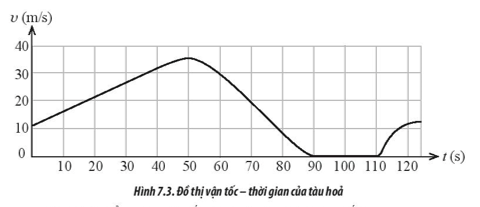
A. Xe C chuyển động đều, còn các xe còn lại là chuyển động biến đổi đều. B. Chỉ có xe C chuyển động đều và chuyển động của xe A là biến đổi đều. C. Xe A và B chuyển động biến đổi đều, xe C chuyển động đều. D. Xe D chuyển động biến đổi đều, xe C chuyển động đều. Phương pháp giải: Vận dụng kiến thức về dạng đồ thị của các loại chuyển động khác nhau. Lời giải chi tiết: Dựa vào hình vẽ đồ thị, ta thấy rằng xe A và xe B chuyển động biến đổi đều (đồ thị vận tốc – thời gian là các đường thẳng không song song với trục hoành), xe C chuyển động đều (đồ thị vận tốc – thời gian là đường thẳng song song với trục hoành). => Chọn C Tự luận 7.1 Tốc độ của một vật có thể tăng trong khi gia tốc của vật đang giảm hay không? Giải thích. Phương pháp giải: Vận dụng kiến thức về gia tốc. Lời giải chi tiết: Tốc độ của một vật có thể tăng trong khi gia tốc của vật đang giảm trong trường hợp vật chuyển động nhanh dần (không đều), chỉ cần vectơ gia tốc cùng hướng với chiều chuyển động của vật. Tự luận 7.2 Trong các chuyển động sau đây, chuyển động nào có giá trị gia tốc không phải là một hằng số trong suốt quá trình chuyển động? a) Một người đi xe đạp đang tăng tốc đều trên đường thẳng từ trạng thái đứng yên. b) Một quả bóng nằm yên trên bàn. c) Một thang máy chuyển động từ tầng 2 lên tầng 4 và có dừng đón khách tại tầng 3? Hãy giải thích các câu trả lời mà em đưa ra. Phương pháp giải: Vận dụng kiến thức về gia tốc. Lời giải chi tiết: a) Người đi xe đạp có gia tốc là một hằng số vì đang chuyển động thẳng nhanh dần đều. b) Quả bóng có gia tốc là một hằng số (bằng 0) vì quả bóng không thay đổi trạng thái chuyển động. c) Thang máy có gia tốc không phải là một hằng số vì lúc chuyển động nhanh dần, lúc chuyển động chậm dần. Chỉ có trường hợp c là có giá trị gia tốc không phải là một hằng số trong suốt quá trình chuyển động. Tự luận 7.3 Trong một quán ăn có hệ thống đưa thức ăn tự động bằng băng chuyền, một khách hàng đặt món ăn qua hệ thống tự động. Sau đó, đĩa thức ăn được di chuyển từ khu vực bếp đến vị trí khách hàng cách nhau 5 m từ trạng thái nghỉ. Giả sử chuyển động của đĩa thức ăn là nhanh dần đều và biết tốc độ của đĩa thức ăn đến khách hàng là 2 m/s. a) Gia tốc của đĩa thức ăn là bao nhiêu? b) Nếu trường hợp khách hàng đặt một li cocktail, vì chiều cao li và mặt đế của li nhỏ nên li sẽ bị đổ khi gia tốc của nó vượt quá 0,5 m/s2. Tìm tốc độ tối đa mà li có thể đạt được để không bị đổ. Phương pháp giải: Vận dụng công thức độc lập với thời gian trong chuyển động thẳng biến đổi đều: \({v^2} - v_0^2 = 2as\) trong đó v, v0 là vận tốc lúc sau, lúc đầu của vật, a là gia tốc của chuyển động, s là quãng đường vật đi được trong thời gian này. Lời giải chi tiết: Tóm tắt: s = 5 m v0 = 0 v = 2 m/s a) a =? b) a <= 0,5 m/s2 => vmax =? Lời giải: a) Chọn chiều dương là chiều chuyển động của đĩa thức ăn. Gia tốc của đĩa thức ăn là: \(a = \frac{{{v^2} - v_0^2}}{{2s}} = \frac{{{2^2} - {0^2}}}{{2.5}} = 0,4\,m/{s^2}.\) b) Tốc độ tối đa của li cocktail có thể đạt được để không bị đổ là: \({v_{\max }} = \sqrt {2a.s} = \sqrt {2.0,5.5} \approx 2,24\,m/s.\) Tự luận 7.4 Xét hai xe oto đang chuyển động cùng chiều trên đoạn đường cao tốc. Tại một thời điểm bất kì, tốc độ của xe A lớn hơn tốc độ của xe B. Dựa vào dữ kiện này có thể nhận định được gia tốc xe A lớn hơn xe B hay không? Giải thích tại sao. Phương pháp giải: Vận dụng kiến thức về gia tốc chuyển động của vật. Lời giải chi tiết: Không đủ dữ kiện để nhận định xe A có gia tốc lớn hơn xe B vì không biết tốc độ ban đầu của hai xe. Tự luận 7.5 Quan sát đồ thị (v – t) mô tả chuyển động thẳng của tàu hỏa trong Hình 7.3 và trả lời các câu hỏi sau:
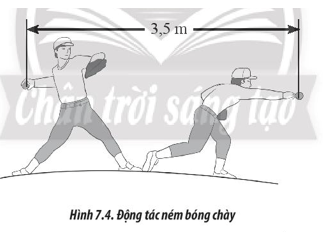
a) Tại thời điểm nào, vận tốc tàu hỏa có giá trị lớn nhất? b) Vận tốc tàu hỏa không đổi trong khoảng thời gian nào? c) Tàu chuyển động nhanh dần đều trong khoảng thời gian nào? Phương pháp giải: Vận dụng cách đọc đồ thị vận tốc – thời gian của vật. Lời giải chi tiết: a) Tại thời điểm t = 50 s, vận tốc tàu hỏa có giá trị lớn nhất (cực đại của đồ thị). b) Trong khoảng thời gian từ 90 s đến 110 s, vận tốc tàu hỏa không đổi (đồ thị vận tốc – thời gian là đoạn thẳng trên trục hoành). c) Trong khoảng thời gian từ 0 đến 40 s, tàu chuyển động nhanh dần đều (đồ thị vận tốc – thời gian là một đoạn thẳng dốc lên). Tự luận 7.6 Giải thích tại sao trong trò chơi bóng chày, cầu thủ ném bóng thường sử dụng tư thế giao bóng như Hình 7.4. Vị trí mà cầu thủ bắt đầu tác dụng lực đến khi quả bóng rời khỏi tay cách nhau một khoảng 3,5 m. Có thể xem gần đúng chuyển động của bóng trong tay cầu thủ trong quá trình giao bóng là chuyển động nhanh dần.
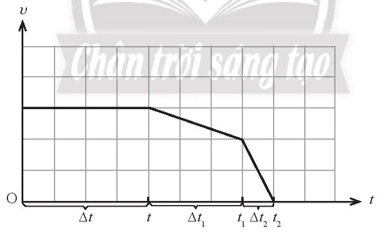
Phương pháp giải: Vận dụng kiến thức của chuyển động thẳng biến đổi đều giải thích hiện tượng trong thực tế. Lời giải chi tiết: Cầu thủ có xu hướng thực hiện động tác như vậy nhằm gia tốc cho quả bóng sau khi rời xa, tốc độ của quả bóng sẽ tăng lên dần nếu chuyển động của quả bóng có thể xem là nhanh dần Tự luận 7.7 Tại hiện trường một vụ tai nạn trên đường quốc lộ ngoài đô thị, cảnh sát phát hiện vết trượt kéo dài 50 m. Qua các đo đạc trên mặt đường, cảnh sát kết luận gia tốc của oto trong quá trình giảm tốc có độ lớn 6,5 m/s2. Nếu tốc độ giới hạn trên làn đường được quy định là 80 km/h thì oto này có vượt quá tốc độ cho phép không? Giả sử trong quá trình giảm tốc, oto chuyển động chậm dần đều. Phương pháp giải: Vận dụng công thức độc lập với thời gian trong chuyển động thẳng biến đổi đều: \({v^2} - v_0^2 = 2as\) trong đó v, v0 là vận tốc lúc sau, lúc đầu của vật, a là gia tốc của chuyển động, s là quãng đường vật đi được trong thời gian này. Lời giải chi tiết: Tóm tắt: s = 50 m a = 6,5 m/s2 v > 80 km/h? Lời giải: Tốc độ của oto là: \(v = \sqrt {2a.s} = \sqrt {2.6,5.50} \approx 25,5\,m/s \approx 91,8\,km/h\), nên trên làn đường này oto đã vượt quá tốc độ cho phép. Tự luận 7.8 Một xe tải đang chuyển động đều với tốc độ cho phép trên đường cao tốc trong khoảng thời gian \(\Delta t\). Khi nhìn thấy biển báo “Đoạn đường hay xảy ra tai nạn”, tài xế quyết định giảm tốc độ. Sau khoảng thời gian \(\Delta {t_1}\), tài xế quan sát thấy một tai nạn đột ngột xảy ra ở phía trước. Do đó tài xế hãm phanh gấp để dừng lại trong khoảng thời gian ngắn \(\Delta {t_2}\) để tránh va chạm. Giả sử trong suốt quá trình chuyển động, xe tải luôn chạy trên đường thẳng. a) Vẽ đồ thị vận tốc – thời gian biểu diễn quá trình chuyển động của xe tải. b) Độ dốc của đồ thị trong trường hợp nào lớn nhất? Phương pháp giải: Vận dụng kiến thức của chuyển động thẳng biến đổi đều giải thích hiện tượng trong thực tế. Lời giải chi tiết: a) Đồ thị vận tốc – thời gian biểu diễn quá trình chuyển động của xe tải.
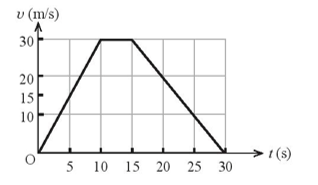
b) Trong thời gian hãm phanh gấp \(\left( {\Delta {t_2}} \right)\) thì độ dốc của đồ thị vận tốc – thời gian là lớn nhất. Tự luận 7.9 Để khảo sát mức độ ảnh hưởng đến sức khỏe của các phi công trên tàu vũ trụ, cũng như máy bay phản lực. Năm 1954, các nhà khoa học thực hiện một nghiên cứu trên tình nguyện viên John P. Stapp. Khảo sát được thực hiện trên một chiếc xe trượt được gia tốc dọc đường ray từ trạng thái đứng yên đến tốc độ 282,5 m/s. Sau đó, chiếc xe trượt được hãm phanh đến khi dừng lại hẳn trong 1,4 s. Mô tả quá trình chuyển động của xe trượt. Phương pháp giải: Vận dụng kiến thức của chuyển động thẳng biến đổi đều giải thích hiện tượng trong thực tế. Lời giải chi tiết: Ban đầu xe trượt chuyển động nhanh dần (từ 0 đến 282,5 m/s), sau đó xe trượt chuyển động chậm dần (từ 282,5 m/s về 0). Tự luận 7.10 Xét một người đi xe máy trên một đoạn đường thẳng. Tốc độ của xe máy tại mỗi thời điểm được ghi lại trong bảng dưới đây.
a) Vẽ đồ thị vận tốc – thời gian của xe máy. b) Nhận xét tính chất chuyển động của xe máy. c) Xác định gia tốc của xe máy trong 10 s đầu tiên và trong 15 s cuối cùng. d) Từ đồ thị vận tốc – thời gian, tính quãng đường mà người này đã đi được 30 s kể từ lúc bắt đầu chuyển động. Phương pháp giải: Vận dụng kiến thức về đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều. Lời giải chi tiết: a) Đồ thị vận tốc – thời gian của xe máy.
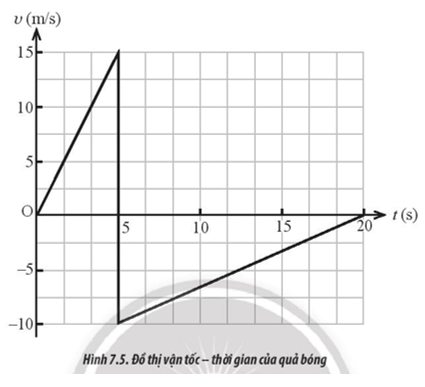
b) Trong khoảng thời gian từ 0 đến 10 s: Xe chuyển động thẳng nhanh dần đều. Trong khoảng thời gian từ 10 s đến 15 s: Xe chuyển động thẳng đều. Trong khoảng thời gian từ 15 s đến 30 s: Xe chuyển động thẳng chậm dần đều. c) Trong 10 s đầu tiên, gia tốc \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30 - 0}}{{10 - 0}} = 3\,m/{s^2}.\) Trong 15 s cuối cùng, gia tốc \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 30}}{{30 - 15}} = - 2\,m/{s^2}.\) d) Quãng đường đi được trong 30 s bằng diện tích giới hạn bởi các đường v(t), v = 0, t = 0, t = 30 s: \(s = \frac{1}{2}.10.30 + \left( {15 - 10} \right).30 + \frac{1}{2}.30.\left( {30 - 15} \right) = 525\left( m \right)\) Tự luận 7.11 Một quả bóng bàn được bắn ra theo phương ngang với vận tốc đầu bằng không đến va chạm vào tường và bật lại trong khoảng thời gian rất ngắn. Hình 7.5 là đồ thị (v – t) mô tả chuyển động của quả bóng trong 20 s đầu tiên. Tính quãng đường mà quả bóng bay được trong 20 s kể từ lúc bắt đầu chuyển động.
Phương pháp giải: Độ dịch chuyển của vật trong khoảng thời gian từ t1 đến t2 được xác định bằng phần diện tích giới hạn bởi các đường v(t), v = 0, t = t1, t = t2 trong đồ thị (v – t). Lời giải chi tiết: Quãng đường mà quả bóng bay được sau 20 s kể từ lúc bắt đầu để chuyển động: \(s = {s_1} + {s_2} = \frac{1}{2}.5.15 + \frac{1}{2}.\left( {20 - 5} \right).10 = 112,5\,m.\) Tự luận 7.12 Một xe chuyển động chậm dần đều với tốc độ 36 km/h. Trong giây thứ 6 xe đi được 7,25 m. Tính quãng đường xe đi được trong giây thứ 8. Phương pháp giải: Vận dụng kiến thức về mối liên hệ giữa quãng đường, gia tốc, vận tốc và thời gian của vật đi trong quá trình chuyển động thẳng biến đổi đều: \(S = {v_0}t + \frac{1}{2}a{t^2}\) Lời giải chi tiết: Quãng đường xe đi được trong giây thứ 6: \({s_6} = {v_0}.6 + \frac{{a{{.6}^2}}}{2} - {v_0}.5 - \frac{{a{{.5}^2}}}{2} = 7,25\,m.\) Suy ra: a = - 0,5 m/s2. Quãng đường xe đi được trong giây thứ 8: \({s_8} = {v_0}.8 + \frac{{a{{.8}^2}}}{2} - {v_0}.7 - \frac{{a{{.7}^2}}}{2} = 6,25\,m.\)
|