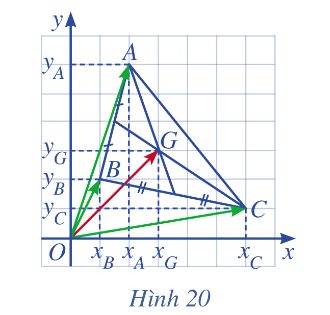
Giải mục II trang 69 SGK Toán 10 tập 2 - Cánh diều

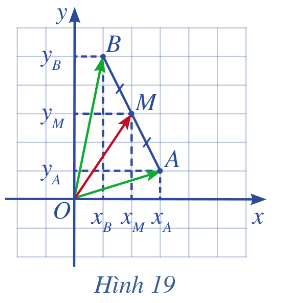
Hoạt động 2

Trong mặt phẳng tọa độ Oxy, cho hai điểm $A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)$. Gọi $M\left( {{x_M},{y_M}} \right)$ là trung điểm của đoạn thẳng AB ( minh họa hình 19)

a) Biểu diễn vectơ $\overrightarrow {OM}$ theo hai vectơ $\overrightarrow {OA}$ và $\overrightarrow {OB}$

b) Tìm tọa độ của M theo tọa độ của A và B

Lời giải chi tiết:

a) Ta có vectơ $\overrightarrow {OM}$  biểu diễn theo hai vectơ $\overrightarrow {OA}$ và $\overrightarrow {OB}$ là: $\overrightarrow {OM}  = \frac{1}{2}\left( {\overrightarrow {OA}  + \overrightarrow {OB} } \right)$

b) Do tọa độ hai điểm A và B là: $A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)$ nên ta có:$\overrightarrow {OA}  = \left( {{x_A},{y_A}} \right),\overrightarrow {OB}  = \left( {{x_B},{y_B}} \right)$

Vậy $\overrightarrow {OM}  = \frac{1}{2}\left( {\overrightarrow {OA}  + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)$

Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M  là $M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)$

Hoạt động 3

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trọng tâm G ( minh họa ở Hình 20)

a) Biểu diễn vectơ $\overrightarrow {OG}$ theo ba vectơ $\overrightarrow {OA}$ , $\overrightarrow {OB}$và $\overrightarrow {OC}$

b) Tìm tọa độ G theo tọa độ của A, B, C

Lời giải chi tiết:

a) Ta có vectơ $\overrightarrow {OG}$ theo ba vectơ $\overrightarrow {OA}$ , $\overrightarrow {OB}$và $\overrightarrow {OC}$ là: $\overrightarrow {OG}  = \frac{1}{3}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right)$

b) Do tọa độ ba điểm A , B và C là: $A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)$ nên ta có:$\overrightarrow {OA}  = \left( {{x_A},{y_A}} \right),\overrightarrow {OB}  = \left( {{x_B},{y_B}} \right),\overrightarrow {OC}  = \left( {{x_C},{y_C}} \right)$

Vậy$\overrightarrow {OG}  = \frac{1}{3}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)$

Tọa độ điểm G chính là tọa độ của vectơ $\overrightarrow {OG}$ nên tọa độ G  là $G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)$

Luyện tập – vận dụng 3

Cho hai điểm A(2; 4) và M(5 ; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB.

Lời giải chi tiết:

Giả sử B có tọa độ: $B\left( {{x_B},{y_B}} \right)$

Do M là trung điểm của đoạn thẳng AB nên: $\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2}\\{y_M} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_A}\\{y_B} = 2{y_M} - {y_A}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2.5 - 2 = 8\\{y_B} = 2.7 - 4 = 10\end{array} \right.$

Vậy tọa độ điểm B là: $B\left( {8;10} \right)$

Luyện tập – vận dụng 4

Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2).

a) Chứng minh ba điểm A, B, G không thẳng hàng.

b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC.

Lời giải chi tiết:

a) Ta có: $\overrightarrow {AB}  = \left( {2;4} \right),\overrightarrow {AG}  = \left( {2;1} \right)$

Do $\overrightarrow {AB}  \ne k.\overrightarrow {AG}$ nên A, B, G không thẳng hàng

b) Giả sử C có tọa độ là: $C\left( {{x_C};{y_C}} \right)$

Để G là trọng tâm tam giác ABC thì: $\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.$

Vậy tọa độ điểm C là: $C\left( {3;0} \right)$