Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức

Hoạt động 7

Cho hàm số \(y = \cot x\)

a) Xét tính chẵn, lẻ của hàm số

b) Hoàn thành bảng giá trị của hàm số \(y = \cot x\) trên khoảng\(\;\left( {0;\pi } \right)\).

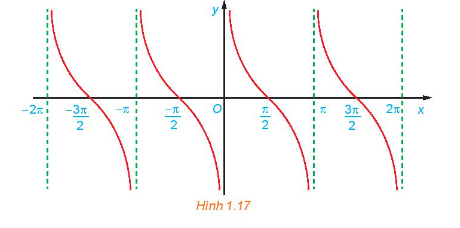
Bằng cách lấy nhiều điểm \(M\left( {x;\cot x} \right)\) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\).

c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \cot x\) như hình dưới đây.

Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số \(y = \cot x\)

Phương pháp giải:

Sử dụng định nghĩa hàm số chẵn lẻ

Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D

Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) =  - \cot x =  - f\left( x \right),\;\forall x\; \in \;D\)

Vậy \(y = \cot x\) là hàm số lẻ.

b)

 c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi  + k\pi } \right)\).

Luyện tập

Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.

Phương pháp giải:

Nhìn đồ thị để xác định vị trí của y và x

Lời giải chi tiết:

Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)