Giải mục 5 trang 71, 72, 73 SGK Toán 11 tập 2 - Chân trời sáng tạo

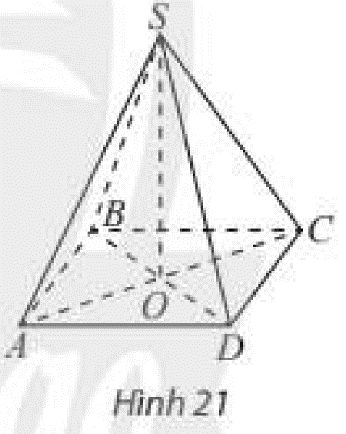
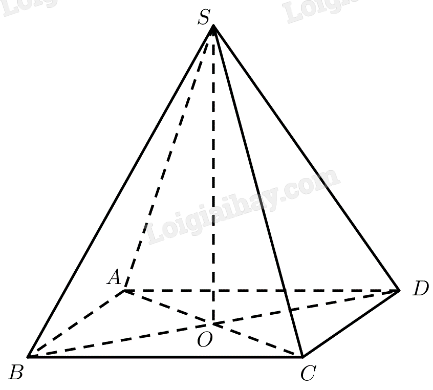
Hoạt động 7

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông với tâm \(O\) và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng \(SO\) có vuông góc với đáy không?

Phương pháp giải:

Sử dụng định lí: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha  \right)\) thì \(d \bot \left( \alpha  \right)\).

Lời giải chi tiết:

Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)

Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)

\( \Rightarrow SO \bot \left( {ABCD} \right)\)

Thực hành 4

Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và \(AB = a,SA = 2a\). Tính \(SO\) theo \(a\).

Phương pháp giải:

Sử dụng định lí Pitago.

Lời giải chi tiết:

 

\(S.ABCD\) là hình chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right)\)

\( \Rightarrow SO \bot AO\)

\(ABC{\rm{D}}\) là hình vuông

\( \Rightarrow AC = AB\sqrt 2  = a\sqrt 2  \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)

Xét tam giác \(SAO\) vuông tại \(O\) có:

\(SO = \sqrt {S{A^2} - A{O^2}}  = \frac{{a\sqrt {14} }}{2}\)

Vận dụng 4

Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136 m và cạnh đáy dài khoảng 152 m. Tính độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp.

(nguồn: https://vi.wikipedia.org/wiki/ Kim tự tháp_Khafre)

Phương pháp giải:

Sử dụng định lí Pitago.

Lời giải chi tiết:

 

Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).

Ta có: \(SO = 136,CD = 152\)

Tam giác \(SCD\) cân tại \(S\)

\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác

\( \Rightarrow I\) là trung điểm của \(CD\).

Mà \(O\) là trung điểm của \(AD\)

\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)

\( \Rightarrow OI = \frac{1}{2}BC = 76\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)

\( \Rightarrow \Delta SOI\) vuông tại \(O\)

\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}}  = 4\sqrt {1517}  \approx 155,8\)

Vậy độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp khoảng 155,8 m.

Hoạt động 8

Cho hình chóp đều \(S.{A_1}{A_2}{A_3}...{A_6}\). Mặt phẳng \(\left( P \right)\) song song với mặt đáy và cắt các cạnh bên lần lượt tại \({A_1}^\prime ,{A_2}^\prime ,{A_3}^\prime ,...,{A_6}^\prime \).

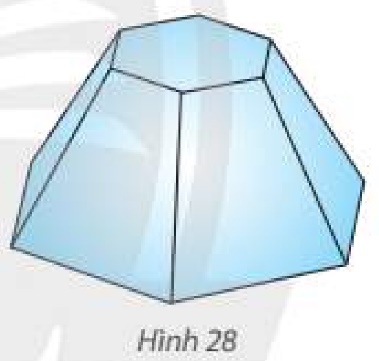
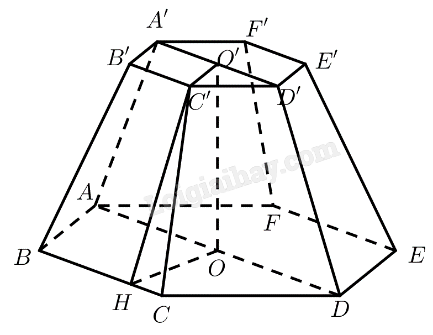
a) Đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) có phải lục giác đều không? Giải thích.

b) Gọi \(O\) và \(O'\) lần lượt là tâm của hai lục giác \({A_1}{A_2}{A_3}...{A_6}\) và \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \). Đường thẳng \(OO'\) có vuông góc với mặt đáy không?

Phương pháp giải:

Sử dụng tính chất của hai mặt phẳng song song.

Lời giải chi tiết:

a) Ta có:

\(\begin{array}{l}\left( P \right)\parallel \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\\ \Rightarrow {A_1}^\prime {A_2}^\prime \parallel {A_1}{A_2},{A_2}^\prime {A_3}^\prime \parallel {A_2}{A_3},{A_3}^\prime {A_4}^\prime \parallel {A_3}{A_4},{A_4}^\prime {A_5}^\prime \parallel {A_4}{A_5},{A_5}^\prime {A_6}^\prime \parallel {A_5}{A_6},{A_6}^\prime {A_1}^\prime \parallel {A_6}{A_1}\\ \Rightarrow \frac{{{A_1}^\prime {A_2}^\prime }}{{{A_1}{A_2}}} = \frac{{{A_2}^\prime {A_3}^\prime }}{{{A_2}{A_3}}} = \frac{{{A_3}^\prime {A_4}^\prime }}{{{A_3}{A_4}}} = \frac{{{A_4}^\prime {A_5}^\prime }}{{{A_4}{A_5}}} = \frac{{{A_5}^\prime {A_6}^\prime }}{{{A_5}{A_6}}} = \frac{{{A_6}^\prime {A_1}^\prime }}{{{A_6}{A_1}}}\end{array}\)

Mà \({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} = {A_5}{A_6} = {A_6}{A_1}\)

\( \Rightarrow {A_1}^\prime {A_2}^\prime  = {A_2}^\prime {A_3}^\prime  = {A_3}^\prime {A_4}^\prime  = {A_4}^\prime {A_5}^\prime  = {A_5}^\prime {A_6}^\prime  = {A_6}^\prime {A_1}^\prime \)

Vậy đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) là lục giác đều.

b) Ta có:

\(\left. \begin{array}{l}O' \in {A_1}^\prime {A_4}^\prime  \subset \left( {S{A_1}{A_4}} \right)\\O' \in {A_3}^\prime {A_6}^\prime  \subset \left( {S{A_3}{A_6}} \right)\\\left( {S{A_1}{A_4}} \right) \cap \left( {S{A_3}{A_6}} \right) = SO\end{array} \right\} \Rightarrow O' \in SO\)

Mà \(S.{A_1}{A_2}{A_3}...{A_6}\) là hình chóp đều \( \Rightarrow SO \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)

Vậy \(OO' \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)

Thực hành 5

Cho hình chóp cụt tam giác đều \(ABC.A'B'C'\) có cạnh đáy lớn \(a\), cạnh đáy nhỏ \(\frac{a}{2}\) và cạnh bên \(2a\). Tính độ dài đường cao của hình chóp cụt đó.

Phương pháp giải:

Dựng đường cao và sử dụng định lí Pitago.

Lời giải chi tiết:

 

Gọi \(O,O'\) lần lượt là tâm của hai đáy \(ABC\) và \(A'B'C'\), \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\).

Kẻ \(A'H \bot AO\left( {H \in AO} \right) \Rightarrow A'H = OO'\)

\(\Delta ABC\) đều \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)

\(\Delta A'B'C'\) đều \( \Rightarrow A'M' = \frac{{\frac{a}{2}.\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4} \Rightarrow A'O' = \frac{2}{3}A'M' = \frac{{a\sqrt 3 }}{6}\)

\(A'HOO'\) là hình chữ nhật \( \Rightarrow OH = A'O' = \frac{{a\sqrt 3 }}{6}\)

\( \Rightarrow AH = AO - OH = \frac{{a\sqrt 3 }}{6}\)

Tam giác \(AA'H\) vuông tại \(H\)

\( \Rightarrow OO' = A'H = \sqrt {AA{'^2} - A{H^2}}  = \frac{{a\sqrt {141} }}{6}\)

Vận dụng 5

Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn.

Phương pháp giải:

Dựng đường cao và sử dụng định lí Pitago.

Lời giải chi tiết:

 

Mô hình hoá hình ảnh cái bục bằng hình chóp cụt lục giác đều \(ABC{\rm{DEF}}{\rm{.}}A'B'C'{\rm{D'E'F'}}\) có \(O\) và \(O'\) là tâm của hai đáy. Kẻ \(C'H \bot BC\left( {H \in BC} \right)\).

Ta có: \(BC = 1;CC' = B'C' = 0,7\).

Diện tích đáy lớn là: \(6.\frac{{B{C^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\)

Diện tích đáy nhỏ là: \(6.\frac{{B'C{'^2}\sqrt 3 }}{4} = \frac{{147\sqrt 3 }}{{200}}\)

\(BCC'B'\) là hình thang cân nên \(HC = \frac{{BC - B'C'}}{2} = 0,15\)

Tam giác \(CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}}  = \frac{{\sqrt {187} }}{{20}}\)

Diện tích một mặt bên là: \(\frac{1}{2}\left( {BC + B'C'} \right).C'H = \frac{{17\sqrt {187} }}{{400}}\)

Diện tích sáu mặt bên là: \(6.\frac{{17\sqrt {187} }}{{400}} = \frac{{51\sqrt {187} }}{{200}}\)

Diện tích cần sơn là: \(\frac{{51\sqrt {187} }}{{200}} + \frac{{3\sqrt 3 }}{2} + \frac{{147\sqrt 3 }}{{200}} \approx 7,36\left( {{m^2}} \right)\)