Giải mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 - Cánh diềuTrong mặt phẳng cho đường thẳng d.
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 5 Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).
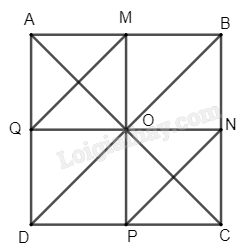
Phương pháp giải: Đường trung trực là đường đi qua trung điểm đoạn thẳng và vuông góc với đoạn thẳng tại trung điểm. Lời giải chi tiết: Cách xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM': - Qua M kẻ đường thẳng d' vuông góc với đường thẳng d tại H. - Trên d', lấy điểm M' sao cho MH = M'H. Khi đó đường thẳng d vuông góc với MM' tại trung điểm H của MM' nên d là đường trung trực của đoạn thẳng MM'. Luyện tập 3 Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC. Phương pháp giải: Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\) Lời giải chi tiết:
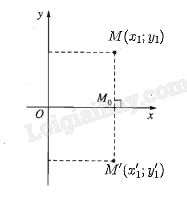
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD. Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA. + Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN. Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M. Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M. Hoạt động 6 Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox. a) Xác định tọa độ của hai điểm M' và N'. b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'. Phương pháp giải: Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\) Lời giải chi tiết: a) Với mỗi điểm M(x1; y1) ta có M'(x1'; y1') là ảnh của điểm M qua phép đối xứng trục Ox thì \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
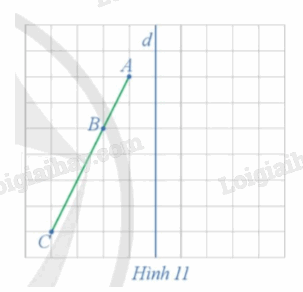
Do đó M'(x1; – y1) và N'(x2; – y2). b) Ta có \(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\M'N' = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {\left( { - {y_2}} \right) - \left( { - {y_1}} \right)} \right)}^2}} \end{array}\) Từ đó suy ra MN = M'N'. Hoạt động 7 Xét phép đối xứng trục d (Hình 11)
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d. b) Nêu mối quan hệ giữa ba điểm A', B', C'. Phương pháp giải: Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\) Lời giải chi tiết: a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d như trên hình vẽ dưới đây.
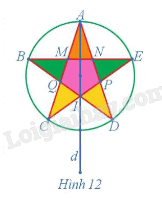
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'. Luyện tập 4 Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
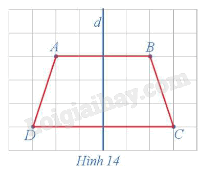
Phương pháp giải: Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\) Lời giải chi tiết: Ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12 là cánh sao màu vàng có các đỉnh C, I, Q. Luyện tập 5 Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox. Phương pháp giải: Tìm ảnh của tâm I qua phép đối xứng trục, sau đó viết phương trình đường tròn (C). Lời giải chi tiết: Ảnh của đường tròn (C) qua phép đối xứng trục Ox là một đường tròn có bán kính R' = R = 2, gọi là (C'). Gọi I' là tâm của đường tròn (C'). Ta có I' là ảnh của I qua phép đối xứng trục Ox, suy ra I'(3; – 2). Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn (C') có tâm I'(3; – 2), bán kính R' = 2. Hoạt động 8 Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14). Tìm ℋ' = Đd(ℋ).
Phương pháp giải: Để tìm ảnh của (H) qua \(Đ_d\) ta tìm ảnh của các điểm thuococj (H) qua \(Đ_d\). Sau đó nối chúng với nhau. Lời giải chi tiết: Đường thẳng d đi qua trung điểm hai háy của hình thang cân ABCD nên đường thẳng d là đường trung trực của các đoạn thẳng AB và CD. Khi đó, ta có phép đối xứng trục d biến các điểm A, B, C, D tương ứng thành các điểm B, A, D, C nên phép đối xứng trục d biến hình thang cân ABCD thành hình thang cân BADC hay hình thang cân ABCD là ảnh của chính nó qua phép đối xứng trục d. Như vậy, ℋ ' ≡ ℋ hay phép đối xứng trục d biến hình ℋ thành chính nó.
|