Giải mục 2 trang 51, 52, 53 SGK Toán 10 tập 2 - Chân trời sáng tạo

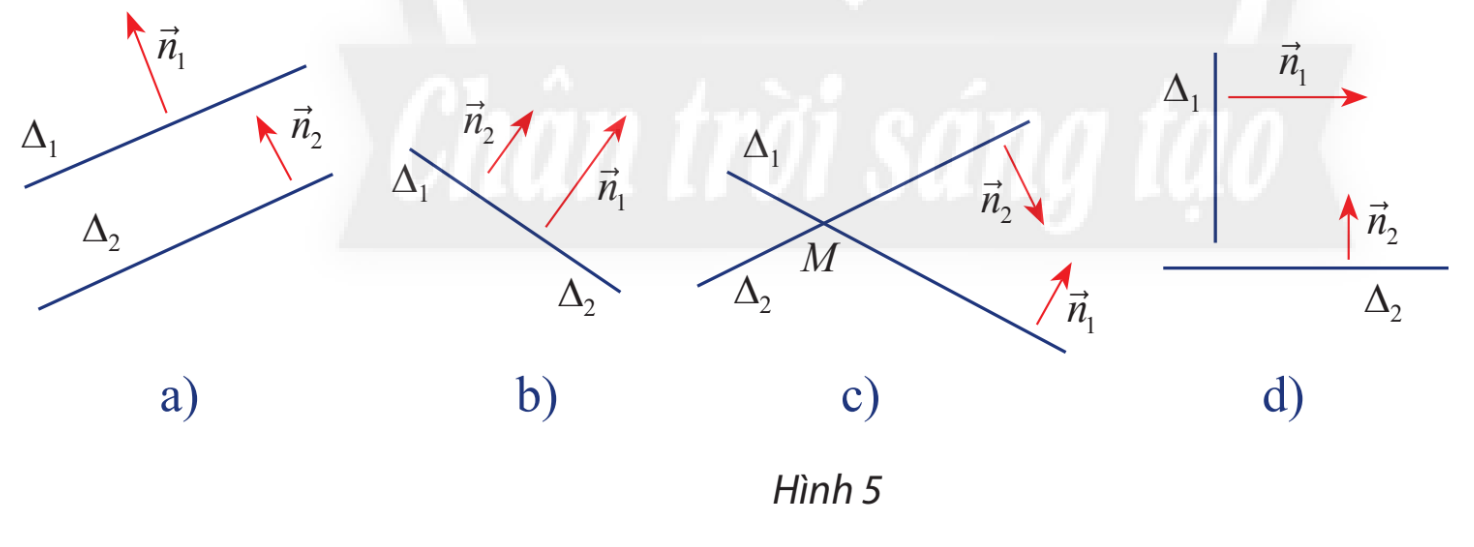
HĐ Khám phá 4

Cho hai đường thẳng ${\Delta _1}$và ${\Delta _2}$ một vectơ pháp tuyến lần lượt là $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$

Nêu nhận xét về vị trí tương đối giữa ${\Delta _1}$và ${\Delta _2}$ trong các trường hợp sau:

a) $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$ cùng phương  (hình 5a,b)

b) $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$ không cùng phương  (hình 5c,d)

c) $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$vuông góc  (hình 5d)

Lời giải chi tiết:

Dựa vào hình vẽ ta có

a) $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$ cùng phương thì hai đường thẳng ${\Delta _1}$và ${\Delta _2}$ song song

b) $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$ không cùng phương thì hai đường thẳng ${\Delta _1}$và ${\Delta _2}$ cắt nhau

c) $\overrightarrow {{n_1}}$ và $\overrightarrow {{n_2}}$ vuông góc thì hai đường thẳng ${\Delta _1}$và ${\Delta _2}$ vuông góc

Thực hành 4

Xét vị trí tương đối của các cặp đường thẳng ${d_1}$và ${d_2}$ trong các trường hợp sau:

a) ${d_1}:x - 5y + 9 = 0$ và ${d_2}:10x + 2y + 7 = 10$

b)  ${d_1}:3x - 4y + 9 = 0$ và ${d_2}:\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 3t\end{array} \right.$

c) ${d_1}:\left\{ \begin{array}{l}x = 5 + 4t\\y = 4 + 3t\end{array} \right.$ và ${d_2}:\left\{ \begin{array}{l}x = 1 + 8t\\y = 1 + 6t\end{array} \right.$

Phương pháp giải:

Bước 1: Xác định cặp vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng

Bước 2: 

+) Nếu 2 vecto cùng phương: Lấy điểm A thuộc d1. Kiểm tra A có thuộc d2 hay không.

=> KL: 2 đường thẳng song song nếu A không thuộc d2.

 2 đường thẳng trùng nhau nếu  A thuộc d2.

+) Nếu 2 vecto không cùng phương: Tính tích vô hướng

Nếu bằng 0 thì hai đường thẳng vuông góc, nếu khác 0 thì 2 đường thẳng chỉ cắt nhau.

=> Giải hệ phương trình từ hai đường thẳng để tìm giao điểm

Lời giải chi tiết:

a) ${d_1}$và ${d_2}$ có vectơ pháp tuyến lần lượt là $\overrightarrow {{n_1}}  = \left( {1; - 5} \right),\overrightarrow {{n_2}}  = \left( {10;2} \right)$

Ta có $\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 1.10 + ( - 5).2 = 0$ nên $\overrightarrow {{n_1}}  \bot \overrightarrow {{n_2}}$

Giải hệ phương trình $\left\{ \begin{array}{l}x - 5y + 9 = 0\\10x + 2y + 7 = 10\end{array} \right.$ ta được nghiệm $\left\{ \begin{array}{l}x =  - \frac{3}{{52}}\\y = \frac{{93}}{{52}}\end{array} \right.$

Suy ra hai đường thẳng ${d_1}$và ${d_2}$ vuông góc và cắt nhau tại $M\left( { - \frac{3}{{52}};\frac{{93}}{{52}}} \right)$

b) ${d_1}$và ${d_2}$ có vectơ pháp tuyến lần lượt là $\overrightarrow {{n_1}}  = \left( {3; - 4} \right),\overrightarrow {{n_2}}  = \left( {3, - 4} \right)$

$\overrightarrow {{n_1}} ,\overrightarrow {{n_2}}$ trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra ${d_1}$và ${d_2}$song song hoặc trùng nhau

Lấy điểm $A(1;1)$ thuộc ${d_2}$, thay tọa độ của A vào phương trình ${d_1}$, ta được $3.1 - 4.1 + 9 = 8 \ne 0$, suy ra A không thuộc đường thẳng ${d_1}$

Vậy hai đường thẳng ${d_1}$và ${d_2}$ song song

c) ${d_1}$và ${d_2}$ có vectơ pháp tuyến lần lượt là $\overrightarrow {{n_1}}  = \left( {3; - 4} \right),\overrightarrow {{n_2}}  = \left( {6; - 8} \right)$

Ta có ${a_1}{b_2} - {a_2}{b_1} = 3.( - 8) - ( - 4).6 = 0$suy ra hai vectơ pháp tuyến cùng phương. Suy ra ${d_1}$và ${d_2}$song song hoặc trùng nhau

Lấy điểm $A(1;1)$ thuộc ${d_2}$, thay tọa độ của A vào phương trình ${d_1}$, ta được $\left\{ \begin{array}{l}1 = 5 + 4t\\1 = 4 + 3t\end{array} \right. \Leftrightarrow t =  - 1$, suy ra A thuộc đường thẳng ${d_1}$

Vậy hai đường thẳng ${d_1}$ và ${d_2}$ trùng nhau

Vận dụng 4

Viết phương trình đường thẳng ${d_1}$:

a) Đi qua điểm $A(2;3)$ và song song với đường thẳng ${d_2}:x + 3y + 2 = 0$

b) Đi qua điểm $B(4; - 1)$ và vuông góc với đường thẳng ${d_3}:3x - y + 1 = 0$

Phương pháp giải:

Bước 1: Từ đường thẳng đã cho xác định vectơ pháp tuyến hoặc vectơ chỉ phương

Bước 2: Viết phương trình tổng quát hoặc phương trình tham số

Lời giải chi tiết:

a) ${d_1}$ song song với đường thẳng ${d_2}:x + 3y + 2 = 0$ nên nhận vectơ pháp tuyến của đường thẳng ${d_2}$ làm vectơ pháp tuyến là $\overrightarrow n  = \left( {1;3} \right)$

${d_1}$ đi qua điểm $A(2;3)$ nên ta có phương trình tổng quát

          $\left( {x - 2} \right) + 3.\left( {y - 3} \right) = 0 \Leftrightarrow x + 3y - 11 = 0$

b) ${d_1}$ vuông góc với đường thẳng ${d_3}:3x - y + 1 = 0$ nên nhận vectơ pháp tuyến của đường thẳng ${d_3}$ làm vectơ chỉ phương là $\overrightarrow u  = \left( {3; - 1} \right)$

${d_1}$ đi qua điểm $B(4; - 1)$ nên ta có phương trình tham số: $\left\{ \begin{array}{l}x = 4 + 3t\\y =  - 1 - t\end{array} \right.$