Giải mục 2 trang 47, 48, 49 SGK Toán 7 tập 1 - Kết nối tri thức1. Quan sát Hình 3.22 và giải thích vì sao AB // CD. 2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song? Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên...
Lựa chọn câu để xem lời giải nhanh hơn
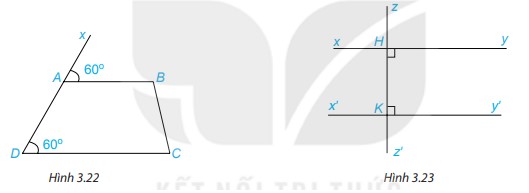
Luyện tập 2 1. Quan sát Hình 3.22 và giải thích vì sao AB // CD. 2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
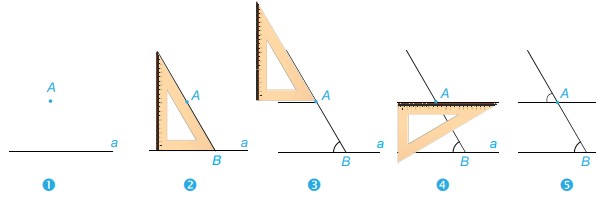
Phương pháp giải: Đường thẳng c cắt hai đường thẳng phân biệt, tạo thành một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song Lời giải chi tiết: 1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\) Mà 2 góc này ở vị trí đồng vị \( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song) 2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù) \(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\) Vì \(\widehat {yHz'} = \widehat {y'Kz'}\) Mà 2 góc này ở vị trí đồng vị \( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song) Chú ý: 2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song. Thực hành 1 Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Để vẽ đường thẳng b đi qua A và song song với a, ta có thể sử dụng góc nhọn \(60^\circ \) của êke để vẽ như sau:
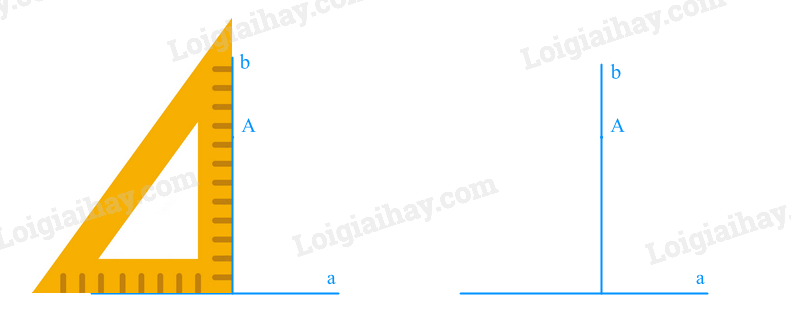
Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song song với nhau. Phương pháp giải: Sử dụng dấu hiệu nhận biết 2 đường thẳng song song Lời giải chi tiết: Ta thấy, khi vẽ hình như trên, ta đã vẽ 2 góc A và B có số đo bằng nhau (đều bằng \(60^\circ \)). Mà 2 góc này ở vị trí đồng vị Vậy a//b (Dấu hiệu nhận biết 2 đường thẳng song song) Thực hành 2 Dùng góc vuông hay góc 30\(^\circ \)của êke (thay cho góc 60\(^\circ \)) để vẽ đường thẳng đi qua và song song với đường thẳng a cho trước. Phương pháp giải: Đặt góc vuông hay góc 30\(^\circ \) của êke thay cho góc 60\(^\circ \) trong Thực hành 1 Lời giải chi tiết: + Dùng góc vuông: Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
Bước 2: Đặt ê ke sao cho 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, 1 cạnh góc vuông còn lại đi qua điểm A, ta kẻ đường thẳng b đi qua A, vuông góc với a.
Bước 3: Kẻ đường thẳng đi qua A, vuông góc với đường thẳng b. Ta được đường thẳng b' đi qua A và song song với a.
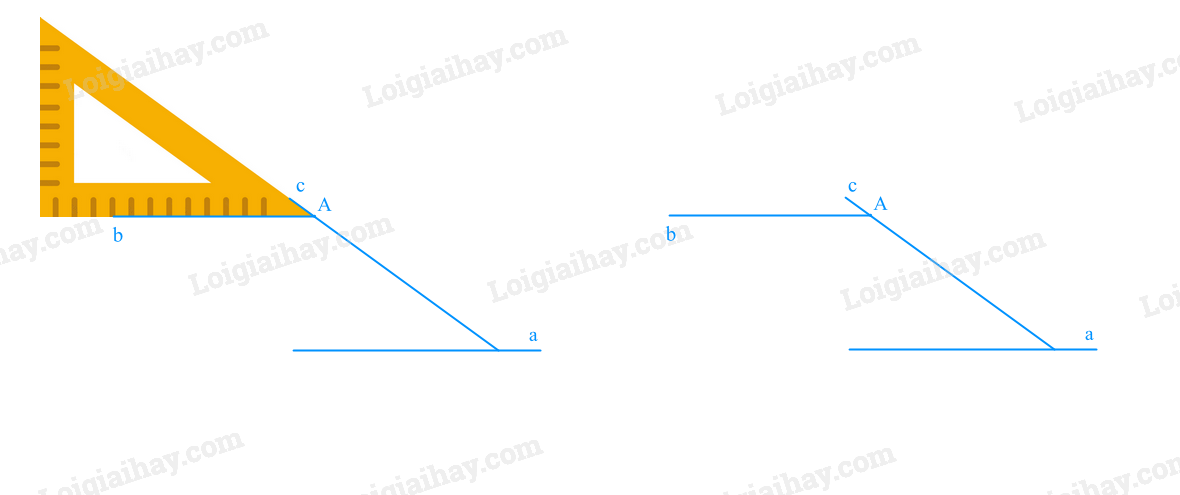
+ Dùng góc 30\(^\circ \)của êke: Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
Bước 2: Đặt ê ke sao cho góc nhọn 30\(^\circ \) và 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, cạnh đối diện với góc vuông đi qua điểm A, ta kẻ đường thẳng c đi qua cạnh đối diện với góc vuông của ê ke.
Bước 3: Dịch chuyển ê ke theo đường thẳng c cho đến khi điểm A trùng với đỉnh của góc nhọn 30\(^\circ \).
Bước 4: Kẻ đường thẳng b đi qua A và 1 cạnh của góc 30\(^\circ \)
Ta được đường thẳng b đi qua A và song song với a.
|