Giải mục 2 trang 44 Chuyên đề học tập Toán 10 - Chân trời sáng tạo

HĐ2

Cho điểm $M(x;y)$nằm trên elip (E): $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ có hai tiêu điểm ${F_1}( - c;0),{F_2}(c;0)$ (Hình 6).

a) Tính ${F_1}{M^2}$ và ${F_2}{M^2}$ theo $x,y,c.$

b) Chứng tỏ rằng ${F_1}{M^2} - {F_2}{M^2} = 4cx,\;{F_1}M - {F_2}M = 2\frac{{cx}}{a}$

c) Tính độ dài hai đoạn $M{F_1},M{F_2}$ theo $a,c,x.$

Lời giải chi tiết:

a) Ta có: $\overrightarrow {M{F_1}} ( - c - x; - y);\overrightarrow {M{F_2}} (c - x; - y)$

$\Rightarrow M{F_1}^2 = {( - c - x)^2} + {( - y)^2};M{F_2}^2 = {(c - x)^2} + {( - y)^2}$

b) ${F_1}{M^2} - {F_2}{M^2} = {( - c - x)^2} - {(c - x)^2} = 4cx$

Mà ${F_1}M + {F_2}M = 2a$ (do $M \in (E)$)

$\Rightarrow \;{F_1}M - {F_2}M = \frac{{{F_1}{M^2} - {F_2}{M^2}}}{{{F_1}M + {F_2}M}} = 2\frac{{cx}}{a}$

 c)

$\begin{array}{l}M{F_1} = \frac{{2a + \frac{{2c}}{a}x}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{2a - \frac{{2c}}{a}x}}{2} = a - \frac{c}{a}x\end{array}$

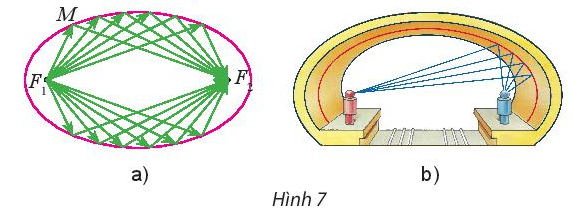
Thực hành 2

a) Tính độ dài hai bán kính qua tiêu của điểm $M(x,y)$ trên (E): $\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1$

b) Tìm các điểm trên elip (E): $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ có độ dài hai bán kính qua tiêu bằng nhau.

Phương pháp giải:

Cho PTCT: $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$

Độ dài bán kính qua tiêu của điểm $M(x,y)$ trên (E) là:

$M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.$

Lời giải chi tiết:

a) Ta có: ${a^2} = 64,{b^2} = 36 \Rightarrow a = 8,b = 6 \Rightarrow c = \sqrt {{a^2} - {b^2}}  = 2\sqrt 7$

Độ dài hai bán kính qua tiêu của điểm $M(x,y)$ là:

$M{F_1} = 8 + \frac{{\sqrt 7 }}{4}x;M{F_2} = 8 - \frac{{\sqrt 7 }}{4}x.$

b) Độ dài bán kính qua tiêu của điểm $M(x,y)$ trên (E) là:

$M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.$

Để độ dài hai bán kính qua tiêu bằng nhau thì $a + \frac{c}{a}x = a - \frac{c}{a}x$

$\Leftrightarrow \frac{c}{a}x =  - \frac{c}{a}x \Leftrightarrow x = 0$

Mà $M(x,y) \in (E)$ $\Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Leftrightarrow y =  \pm b$

Vậy tại các điểm ${B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)$ thì độ dài hai bán kính qua tiêu bằng nhau.

Vận dụng 2

Người ta chứng minh được rằng ánh sáng hay âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu (Hình 7a).

Vòm xe điện ngầm của một thành phố có mặt cát hình elip (Hình 7b). Hãy giải thích tại sao tiếng nói của một người phát ra từ một tiêu điểm bên này, mặc dù khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.

Phương pháp giải:

Cho elip (E): $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$

Với M bất kì thuộc Elip, ta luôn có: $M{F_1} + M{F_2} = 2a$

Lời giải chi tiết:

Gọi PTCT của elip biểu diễn vòm xe điện ngầm là:  $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$

Với M bất kì thuộc Elip, ta luôn có: $M{F_1} + M{F_2} = 2a$

Nói cách khác tiếng nói phát ra từ một tiêu điểm bên này, khi đi đến các điểm khác nhau trên elip vẫn luôn tới tiêu điểm bên kia với cùng một quãng đường là $2a$.

Do đó tiếng nói vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.